Bất phương trình: 32 x - 8 + 2 x > 2 tương đương với bất phương trình
A. 20 x > 2 B. 2 5 > 2
C. 15 2 x > 2 D. 2 x > 2
Hãy chọn đáp án đúng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: D
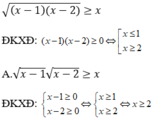
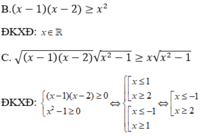
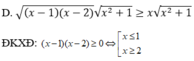
Ta thấy, bất phương trình đã cho và bất phương trình ở đáp án D có cùng tập xác định. Do đó, hai bất phương trình này sẽ có cùng tập nghiệm.
Chú ý: Hai bất phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm. Nếu sử dụng các phép biến đổi không làm thay đổi tập nghiệm của bất phương trình sẽ cho ta bất phương trình tương đương. Việc thay đổi tập xác định có thể làm thay đổi tập nghiệm của bất phương trình.

Ta có x - 2 < 1 Û x - 2 + 1 < 1 + 1 Û x - 1 < 2
Chuyển vế -2 từ vế trái sang vế phải thì phải đổi dấu ta được
Bpt Û x < 1 + 2 Û x < 3 => loại đáp án A và B.
Đáp án cần chọn là: D

3x - 2(y - x + 1) > 0 ⇔ 3x - 2y + 2x - 2 > 0 ⇔ 5x - 2y - 2 > 0
Đáp án là B.

Ta có: x + 3 < 1 Û x + 3 + (-3) < 1 + (-3) Û x < -2.
Đáp án cần chọn là: C

Nếu nhân hai vế của 1/x ≤ 1 với x, ta được bất phương trình mới x ≥ 1; bất phương trình này không tương đương với bất phương trình đã cho vì đã làm mất đi tất cả các nghiệm âm của nó.
Ghi nhớ: Không được nhân hay chia hai vế của một bất phương trình với một biểu thức chứa ẩn mà không biết dấu của biểu thức đó.

Thử trực tiếp ta thấy ngay x = -3 là nghiệm của bất phương trình (1) nhưng không là nghiệm bất phương trình (2), vì vậy (1) và (2) không tương đương do đó phép bình phương hai vế một bất phương trình không phải là phép biến đổi tương đương.

Đáp án B.
Ta thấy bất phương trình ở đề bài và bất phương trình (x - 1 ) 2 (x + 5) ≥ 0 cùng có tập nghiệm là: [-5; + ∞ ). Do đó, hai bất phương trình này tương đương với nhau
Chọn đáp án D