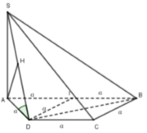
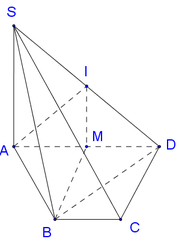
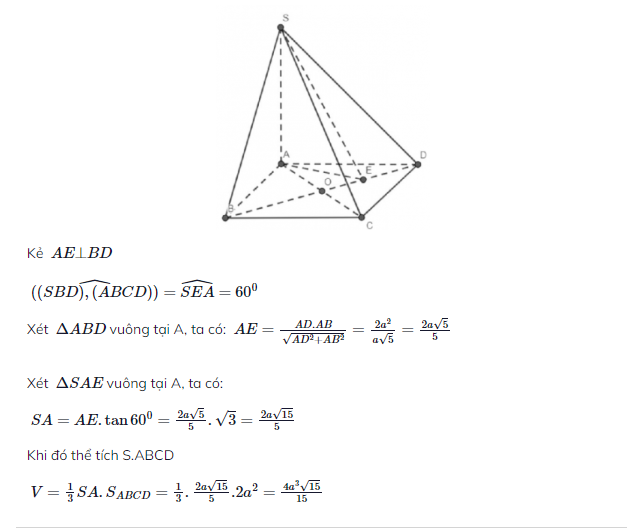
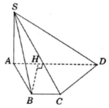
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, đáy lớn AB. Biết rằng AB= 2a, AD = DC = CB = a, cạnh bên SA vuông góc với đáy, mặt phẳng (SBD) tạo với đáy một góc 45 0 Gọi O là trung điểm AB. Tính khoảng cách d từ điểm O đến mặt phẳng (SBD).
A. d = a 2 4
B. d = a 4
C. d = a 2
D. d = a 2 2

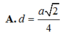
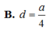
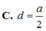
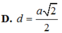

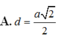
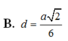
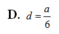

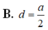
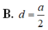
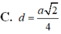
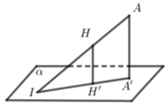
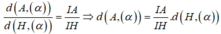



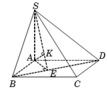
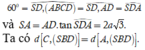
Chọn A