Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
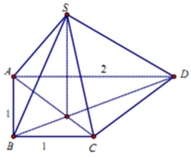
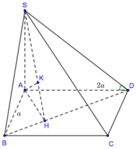
Chứng minh được ∆ S A D vuông cân tại A và ∆ A B D vuông tại D.
Khi đó d G , S B D = 1 3 d A , S B D = a 2 6 .

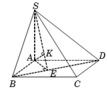
Xác định
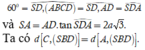
![]()
Tam giác vuông BAD có ![]()
Tam giác vuông SAE có ![]()
![]()
Chọn A.

Đáp án D
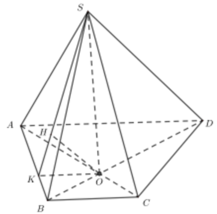
Đặt A D = x x > 0 . Gọi J là trung điểm BD ta có IS ⊥ I D ; I S ⊥ I J ; I D ⊥ I J .
Tứ diện SIJD vuông tại I. Gọi h là khoảng cách từ I đến mặt phẳng S B D ta có.
1 = 1 h 2 = 1 S I 2 + 1 I D 2 + 1 I J 2 = 1 x 3 2 2 + 1 x 2 2 + 1 x 2 2 + 1 x ⇒ h = 57 19 x .
Từ giả thiết ⇒ x = 57 3 c m
Vậy S A B C D = 1 2 A B + D C . A D = 19 2

Đáp án C
Theo dữ kiện đề bài cho, dễ dàng chứng minh được ΔACD vuông tại cân C và A C = A D 2 = a 2 .
C D ⊥ A C C D ⊥ S A ⇒ C D ⊥ S A C ⇒ S A C ⊥ S C D
Mà S A C ∩ S C D = S C , từ A kẻ A H ⊥ S C . Khi đó d A ; S C D = A H .
Tam giác SAC vuông tại
A: 1 A H 2 = 1 S A 2 + 1 A C 2 = 1 a 2 + 1 2 a 2 = 3 2 a 2 ⇒ d A ; S C D = A H = a 2 3
Mặt khác: A D ∩ S C D = D và M là trung điểm AD nên:
d M ; S C D d A ; S C D = M D A D = 1 2 ⇒ d M ; S C D = 1 2 d A ; S C D = a 6 6
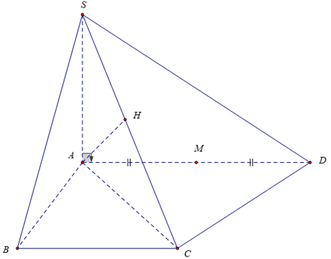

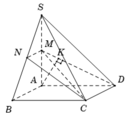
Xác định được ![]()
Vì M là trung điểm SA nên
![]()
Kẻ ![]() và chứng minh được
và chứng minh được ![]() nên
nên ![]()
Trong
∆
vuông MAD tính được ![]()
Chọn A.

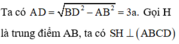
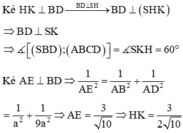



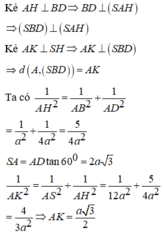
Chọn A