Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(ab=ƯCLN\left(a,b\right)\cdot BCNN\left(a,b\right)=3\cdot84=252\\ ƯCLN\left(a,b\right)=3\Leftrightarrow\left\{{}\begin{matrix}a=3k\\b=3q\end{matrix}\right.\left(k,q\in N\right)\\ \Leftrightarrow3k\cdot3q=252\\ \Leftrightarrow kq=\dfrac{252}{9}=28\)
Mà \(\left(k,q\right)=1\Leftrightarrow kq=1\cdot28=4\cdot7\)
Ta có bảng
| k | 1 | 28 | 4 | 7 |
| q | 28 | 1 | 7 | 4 |
| a | 3 | 81 | 12 | 21 |
| b | 84 | 3 | 21 | 12 |
Vậy ...




1.
\(ƯCLN\left(a,b\right)=7\)
\(\Rightarrow a,b\)chia hết cho 7
\(\Rightarrow a,b\in B\left(7\right)\)
\(B\left(7\right)=\left(0;7;14;21;28;35;42;49;56;63;70;77;84;91;98;105...\right)\)
a, vì a+b=56 \(\Rightarrow\)\(a\le56;b\le56\)
\(\Rightarrow a=56;b=0.a=0;b=56\)
\(a=7;b=49.a=49;b=7\)
\(a=14;b=42.a=42;b=14\)
\(a=21;b=35.a=35;b=21\)
\(a=b=28\)
b, a.b=490 \(\Rightarrow a< 490;b< 490\)
\(\Rightarrow\) \(a=7;b=70-a=70;b=7\)
\(a=14;b=35-a=35;b=14\)
c, BCNN (a,b) = 735
\(\Rightarrow a,b\inƯ\left(735\right)\)
\(Ư\left(735\right)=\left(1;3;5;7;15;21;35;49;105;147;245;735\right)\)
\(\Rightarrow\)\(a=7;b=105-a=105;b=7\)
2.
a+b=27\(\Rightarrow\)\(a\le27;b\le27\)
ƯCLN(a,b)=3
\(\Rightarrow a,b\in B\left(_{ }3\right)\in\left(0;3;6;9;12;15;18;21;24;27;30;...\right)\)
BCNN(a,b)=60
\(\Rightarrow a,b\inƯ\left(60\right)\in\left(1;2;3;4;5;6;10;12;15;20;60\right)\)
\(\Rightarrow\)\(a=12;b=15-a=15;b=12\)

a, Gọi hai số phải tìm là a,b. Ta có (a;b) = 6 => a = 6a’, b = 6b’ với (a’,b’) = 1(a,b,a’,b’ ∈ N)
Do đó: a+b = 84 => 6.(a’+b’) = 84 => a’+b’ = 14
Chọn cặp số a’,b’ là hai số nguyên tố cùng nhau có tổng bằng 14 ta được:
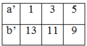
Do đó:
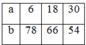
b, Gọi hai số phải tìm là a.b. Ta có (a;b) = 5 => a = 5a’, b = 5b’ với (a’,b’) = 1 (a,b,a’,b’ ∈ N)
Do ab = 300 => 25a’b’ = 300 => a’b’ = 12 = 4.3
Chọn cặp số a’,b’ nguyên tố cùng nhau có tích bằng 12 ta được:
a’ = 1, b’ = 12 => a = 5, b = 60
a’ = 3, b’ = 4 => a = 15, b = 20
c, Gọi hai số phải tìm là a,b. Ta có (a;b) = 10 => a = 10a’; b = 10b’ với (a’,b’) = 1 (a,b,a’,b’ ∈ N, a’<b’). Do đó: ab = 100a’b’ (1)
Mặt khác: ab = [a,b].(a,b) = 900.10 = 9000 (2)
a’ = 1, b’ = 90 => a = 10, b = 900
a’ = 2, b’ = 45 => a = 20, b = 450
a’ = 5, b’ = 18 => a = 50, b = 180
a’ = 9, b’ = 10 => a = 90, b = 100
Đặt \(a=3m,b=3n\)khi đó \(\left(m,n\right)=1\).
\(ab=\left(a,b\right).\left[a,b\right]=3.84=252\)
\(ab=3m.3n=9mn=252\Leftrightarrow mn=28\)
Vì \(\left(m,n\right)=1\)nên ta có bảng giá trị: