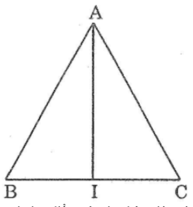
Cắt tam giác ABC bằng giấy có AB = AC và gấp hình theo tia phân giác của góc A. Nếu gấp chia tam giác ABC thành hai tam giác. Hãy đo để kiểm tra xem hai tam giác đó có bằng nhau hay không?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 12 2018
Ta có: góc AB’M là góc ngoài của tam giác MB’C
Nên ∠(BMC) + ∠C= (AB'M) ⇒ ∠(AB'M) > ∠C
5 tháng 2 2022
\(\widehat{xAC}=\dfrac{180^0-\widehat{BAC}}{2}\)
\(\widehat{ACB}=\dfrac{180^0-\widehat{BAC}}{2}\)
Do đó: \(\widehat{xAC}=\widehat{ACB}\)
mà hai góc này ở vị trí so le trong
nên Ax//BC
Gọi giao điểm của tia phân giác góc A vói cạnh BC là I
Ta có: ΔABI=ΔACI