Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

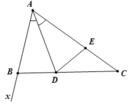
b. Giả sử góc ngoài tại đỉnh B của tam giác ABC là ∠(xBC). Ta có:
∠(xBC) + ∠(ABD) = 180o ⇒ ∠(xBC) = 180o - ∠(ABD) (0.5 điểm)
∠(DEC) + ∠(AED) = 180o ⇒ ∠(DEC) = 180o - ∠(AED) (0.5 điểm)
Mà ∠(ABD) = ∠(AED) ( hai góc tương ứng vì ΔABD = ΔAED)(0.5 điểm)
Từ đó suy ra ∠(xBC) = ∠(DEC) (0.5 điểm)

Câu 1:
a) So sánh ∠B và ∠C ?
Vì AB < AC (gt) ⇒ ∠C < ∠B
b) So sánh BH và CH ?
Trên ta BC lấy điểm D sao cho BH = HD
Xét hai tam giác vuông ABH và ADH có:
BH = DH (gt)
AH : cạnh chung
Do đó: ΔABH = ΔADH (hai cạnh góc vuông)
⇒ BH = HD (hai cạnh tương ứng)
Mà CH = CD + DH ( do D nằm giữa H và C)
⇒ CH > BH .
Câu 2 để tớ đi học về rồi làm cho ~

a) xét tam giác ABH và tam giác ADH
Có góc BAH = Góc DAH (gt)
Ad cạnh chung
góc BHA = góc DHA = 90 độ
Vậy 2 tam giác đó = nhau => AB = AD => tam giác ABD cân tại A
b/

CM: a) Xét t/giác ABM và t/giác AEM
có AB = AE (gt)
góc BAM = góc EAM (gt)
AM : chung
=> t/giác ABM = t/giác AEM (c.g.c) (Đpcm)
b) Ta có: t/giác ABM = t/giác AEM (cmt)
=> BM = ME (hai cạnh tương ứng)
c) Xét t/giác ABH và t/giác AEH
có AB = AE (gt)
góc BAH = góc HAE (gt)
AH : chung
=> t/giác ABH = t/giác AEH (c.g.c)
=> góc BHA = góc AHE (hai góc tương ứng)
Mà góc BHA + góc AHE = 1800 (kề bù)
=> 2.góc BHA = 1800
=> góc BHA = 1800 : 2
=> góc BHA = 900
=> AH \(\perp\)BE (Đpcm)
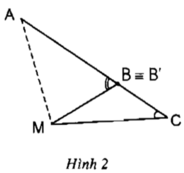
Ta có: góc AB’M là góc ngoài của tam giác MB’C
Nên ∠(BMC) + ∠C= (AB'M) ⇒ ∠(AB'M) > ∠C