Trong không gian Oxyz cho đường thẳng d có phương trình x − 3 1 = y − 1 1 = z 2 và mặt cầu (S) có phương trình x 2 + y 2 + z 2 + 2 x − 2 y + 2 z − 1 = 0 . (P) và (Q) là hai mặt phẳng chứa d và cắt (S) theo các đường tròn có bán kính bằng 1. Tính cosin của góc giữa (P) và (Q).
A. 5 11
B. 4 6 11
C. 5 33
D. 2 266 33

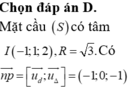
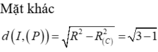
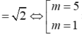

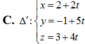
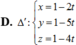


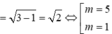


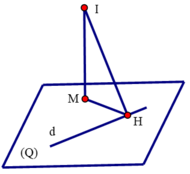
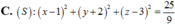


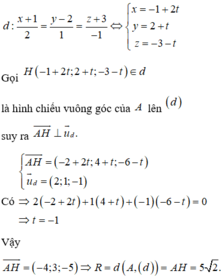

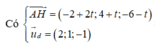
Đáp án A
Đường thẳng d đi qua các điểm M 3 ; 1 ; 0 và N 4 ; 2 ; 2
Xét mặt phẳng (P) có phương trình A x + B y + C z + D = 0
(P) đi qua d khi và chỉ khi (P) đi qua M và N
⇔ 3 A + B + D = 0 4 A + 2 B + 2 C + D = 0 ⇒ C = − A + B 2 D = − 3 A − B
Phương trình (P) trở thành
A x + B y − A + B 2 x − 3 A − B = 0
⇔ 2 A x + 2 B y − A + B z − 6 A − 2 B = 0
Mặt cầu (S) có tâm I − 1 ; 1 ; − 1 và bán kính R = 2 .
Giao tuyến của (P) và (S) là đường tròn có bán kính r=1. Suy ra khoảng cách từ (I) đến (P) là d = R 2 − r 2 = 4 − 1 = 3
Từ đó ta có
− 2 A + 2 B + A + B − 6 A − 2 B 4 A 2 + 4 B 2 + A + B 2 ⇔ − 7 A + B 2 = 3 5 A 2 + 5 B 2 + 2 A B
⇔ 34 A 2 − 20 A B − 14 B 2 = 0 ⇒ 34 A B 2 − 20 A B − 14 = 0 ⇒ A B = 1
hoặc A B = − 7 17
Với A B = 1 ⇒ B = A ta có phương trình (P)
2 A x + 2 A y − 2 A z − 8 A = 0 ⇔ x + y − z − 4 = 0
Với A B = − 7 17 : Chọn A = − 7, B = 17 ta có phương trình (Q): 7 x − 17 y + 5 z − 4 = 0
Gọi α là góc giữa (P) và (Q). Ta có cos α = 1.7 + 1. − 17 − 1.5 1 + 1 + 1 . 49 + 289 + 25 = 5 11 . Ta chọn đáp án A