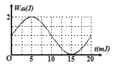
Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của thế năng đàn hồi Wđh của một con lắc lò xo vào thời gian t. Khối lượng vật nặng là 400 g. Lấy π 2 = 10. Biên độ dao động là
A. 2,5 cm.
B. 1 cm.
C. 4 cm.
D. 2 cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Từ đồ thị ta thấy chu kỳ dao động của thế năng đàn hồi là 10.2ms = 20 ms. Suy ra chu kì dao động của con lắc lò xo là T = 2.20s = 40ms = 0,04 s
⇒ f = 1 T = 25 H z

Đáp án B
Từ đồ thị ta thấy chu kỳ dao động của thế năng đàn hồi là 10.2ms = 20 ms. Suy ra chu kì dao động của con lắc lò xo là T = 2.20s = 40ms = 0,04 s
⇒ f = 1 T = 25 H z

Đáp án C
Trên đồ thị ta có:
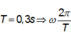
![]()
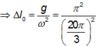
![]() độ biến dạng của lò xo ở VTCB
độ biến dạng của lò xo ở VTCB
Chọn chiều dương hướng xuống, gốc tọa độ O tại VTCB, gốc thế năng tại vị trí lò xo không biến dạng. Biểu thức thế năng đàn hồi: ![]()
Từ đó:
- Tại vị trí ![]() thì
W
t
=
0
thì
W
t
=
0
- Tại vị trí ![]() thì
thì ![]()
Tại vị trí ![]() thì
thì 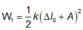
![]()
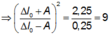
![]()
![]()
![]() ( suy từ các biểu thức thế năng)
( suy từ các biểu thức thế năng)
Và 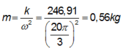

Đáp án A
Vì thời điểm t = 0 , 1 s ở giữa hai thời điểm thế năng đàn hồi bằng 0 nên lúc này vật đang ở vị trí biên âm
Lúc này: W d h 1 = 0 , 3 4 = 0 , 075 J = k A − Δ l 0 2 2
Tại thời điểm t 2 = 0 , 2 s thì lò xo ở biên dương
⇒ W d h 2 = k A + Δ l 0 2 2 = 0 , 6 + 0 , 3 4 = 0 , 675 J
Từ đó suy ra: A − Δ l 0 A + Δ l 0 = 1 3 ⇒ A = 2 Δ l 0 ⇒ k Δ l 0 2 2 = 0 , 075 J
Dễ thấy: T 2 = 0 , 25 − 0 , 1 = 0 , 15 s ⇒ T = 0 , 3 s ⇒ ω = 20 π 3 r a d / s
Nên ω 2 = k m = Δ l 0 g ⇒ Δ l 0 = 9 400 m ⇒ 0 , 075 = k Δ l 0 2 2 = m g Δ l 0 2 ⇒ m = 0 , 667 k g
Đáp án D
*Dựa vào đồ thị ta có thế năng đàn hồi cực đại đến thời điểm gần nhất thế năng đàn hồi cực tiểu tương ứng là