Một con lắc lò xo gồm một vật khối lượng 0,5 kg gắn vào đầu tự do của một lò xo nhẹ có độ cứng 20 N/m. Con lắc dao động theo trục Ox nằm ngang với biên độ dao động là 3 cm. Tính : Động năng và tốc độ của vật tại vị trí có li độ bằng 2,0 cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
5 tháng 1 2018
Cơ năng của con lắc
W = 1/2 .k A 2 = 1/2 .20. 3 . 10 - 2 2 = 9. 10 - 3 J
Tốc độ cực đại của con lắc là
VT
12 tháng 5 2017
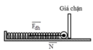
Đáp án B
Phương trình động lực học cho vật theo phương ngang: F d h + N = m a , khi vật rời khỏi giá thì N = 0.
→ Δ l = m a k = 1.3 100 = 0 , 03 m
→ Vật sẽ rời giá chặn tại vị trí lò xo bị nén một đoạn 3 cm
+ Thời gian chuyển động của vật từ vị trí ban đầu đến khi rời khỏi giá t = 2 17 3 − 3 .10 − 2 3 = 2 15 s.
Vận tốc của vật khi rời khỏi giá chặn v = a t = 3 2 15 = 40 cm.
→ Biên độ dao động mới A = 3 2 + 40 10 2 = 5 cm.
VT
29 tháng 10 2017
Biên độ dao động của vật và chiều dài của lò xo khi chưa biến dạng.
A = ( l 1 - l 2 )/2 = (24 - 20)/2 = 2cm
l 0 = l 1 + A = 20 + 2 = 22cm
VT
11 tháng 7 2018
Đáp án C
Cơ năng của con lắc lò xo được xác định bởi biểu thức
TN
22 tháng 3 2020
giải
đổi 3cm=0,03m
a) cơ năng của con lắc lò xo
\(W=\frac{1}{2}.k.A^2=\frac{1}{2}.20.0,03^2=9.10^{-3}\left(J\right)\)
Tốc độ cực đại của con lắc là
\(W=\frac{1}{2}.m.v^2\Rightarrow v_{max}=\sqrt{\frac{2\text{W}}{m}}=\sqrt{\frac{2.9.10^{-3}}{0,5}}=0,19m/s\)
b) đổi 2cm=0,02m
Động năng của vật tại vị trí có li độ bằng 2 là
\(Wt=\frac{1}{2}.kx^2=\frac{1}{2}.20.0,02^2=4.10^{-3}\)
\(Wđ=\)\(W-\)\(Wt=9.10^{-3}-4.10^{-3}=5.10^{-3}\)
Tốc độ của vật tại vị trí có li độ bằng 2,0 cm.
\(v=\sqrt{\frac{2\text{W}\text{ }\text{đ}}{m}}=\sqrt{\frac{2.5.10^{-3}}{0,5}}=0,14\left(m/s\right)\)
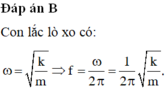
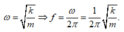
Động năng của vật tại vị trí có li độ bằng 2 là
W t = 1/2 .k x 2 = 1/2 .20. 2 . 10 - 2 2 = 4. 10 - 3
W đ = W - W t = (9 - 4). 10 - 3 = 5. 10 - 3
Tốc độ của vật tại vị trí có li độ bằng 2,0 cm.