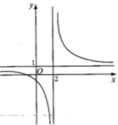
Các đường cong ở hình bên là đồ thị của hàm số y = a x + b c x + d với a,b,c,d là các số thực. Mệnh đề nào sau đây đúng?
A. y ' < 0 , ∀ x ≠ 2
B. y ' < 0 , ∀ x ≠ 1
C. y ' > 0 , ∀ x ≠ 2
D. y ' > 0 , ∀ x ≠ 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Phương pháp: Dựa vào các đường tiệm cận và sự đơn điệu của đồ thị hàm số.
Cách giải: Ta thấy hàm số nghịch biến trên (-∞;2) và (2;+ ∞) => y ' < 0 ∀ x ≠ 2

Đáp án C
Dựa vào đổ thị ta thấy hàm số giảm trên từng khoảng xác định nên
![]()

Đáp án D
Phương pháp giải: Dựa vào hình dáng, đường tiệm cận đồ thị hàm số
Lời giải: Dựa vào hình vẽ, ta thấy đồ thị hàm số có tiệm cận đứng x = 2 và đi xuống
Vậy hàm số nghịch biến trên khoảng − ∞ ; 2 và 2 ; + ∞ ⇒ y ' < 0 , ∀ x ≠ 2

Chọn D
Dựa vào đồ thị ta thấy, hàm số nghịch biến trên các khoảng ![]()
![]()

Quan sát đồ thị hàm số ta thấy, hàm số nghịch biến trên các khoảng
![]()
Chọn: D

Chọn D.
Phương pháp
Quan sát và nhận xét dáng đồ thị hàm số, từ đó suy ra tính đồng biến nghịch biến và dấu của y ' .
Cách giải:
Từ đồ thị hàm số ta thấy hàm số nghịch biến trên các khoảng - ∞ ; 2 và 2 ; + ∞ .
Vậy y ' < 0 , ∀ x ≠ 2 .
Chọn A