Tìm các số thực x, y thỏa mãn: x + 2y + (2x – y)i = 2x + y + (x + 2y)i
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=x^4+y^4-2x^3-2x^2y^2+x^2-2y^3+y^2\)
\(A=\left(x^4-2x^2y^2+y^4\right)-2\left(x^3+y^3\right)+\left(x^2+y^2\right)\)
\(A=\left(x^2-y^2\right)^2-2\left(x^3+y^3\right)+\left(x^2+y^2\right)\)
\(A=\left[\left(x-y\right)\left(x+y\right)\right]^2-2\left(x+y\right)\left(x^2-xy+y^2\right)+\left(x^2+y^2\right)\)
\(A=\left(x-y\right)^2-2\left(x^2-xy+y^2\right)+\left(x^2+y^2\right)\)
\(A=x^2-2xy+y^2-2x^2+2xy-2y^2+x^2+y^2\)
\(A=0\)


Sửa: \(P=2x^4+x^3\left(2y-1\right)+y^3\left(2x-1\right)+2y^4\); x+y=1
Ta có \(P=2x^4+x^3\left(2y-1\right)+y^3\left(2x-1\right)+2y^4=2x^4+2x^3y-x^3+2xy^3-y^3+2y^4\)
\(=x^3\left(2x+2y\right)+y^3\left(2x+2y\right)-\left(x^3+y^3\right)=\left(2x+2y\right)\left(x^3+y^3\right)-\left(x^3+y^3\right)\)
\(=\left(2x+2y-1\right)\left(x^3+y^3\right)=x^3+y^3\)
Do \(x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)=x^2-xy+y^2=\frac{1}{2}\left(x^2+y^2\right)\left(\frac{x}{\sqrt{2}}-\frac{y}{\sqrt{2}}\right)^2\)
\(\Rightarrow P\ge\frac{1}{2}\left(x^2+y^2\right)\)
Mà \(x+y=1\Rightarrow x^2+y^2+2xy=1\Rightarrow2\left(x^2+y^2\right)-\left(x-y\right)^2=1\)
\(\Rightarrow2\left(x^2+y^2\right)\ge1\Rightarrow\left(x^2+y^2\right)\ge\frac{1}{2}\Rightarrow P\ge\frac{1}{4}\)
Dấu "=" xảy ra khi \(x=y=\frac{1}{2}\)
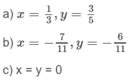
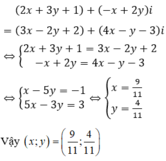
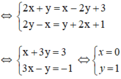
x = y = 0