Xét chiều biến thiên và vẽ đồ thị của các hàm số: y = |x + 1|
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
3 tháng 7 2017
Hàm số 
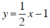có:
+ Tập xác định D = R.
+ Có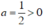 
nên hàm số đồng biến trên R.
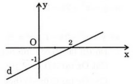
+ Tại x = 0 thì y = 1/2 . 0 – 1 = –1 . Vậy A (0; –1) thuộc đồ thị hàm số.
Tại x = 2 thì y = 1/2 . 2 – 1 = 0. Vậy B (2; 0) thuộc đồ thị hàm số.
Vậy đồ thị hàm số là đường thẳng đi qua hai điểm A (0; –1) và B (2; 0).
PT
1
CM
15 tháng 1 2019
Hàm số 
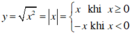có :
+ Tập xác định D = R.
+ Trên (–∞; 0), hàm số y = –x nghịch biến.
Trên (0 ; +∞), hàm số y = x đồng biến.
Bảng biến thiên :
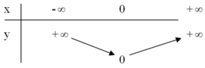
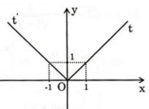
+ Đồ thị hàm số gồm hai phần:
Phần thứ nhất: Nửa đường thẳng y = –x giữ lại phần bên trái trục tung.
Phần thứ hai: Nửa đường thẳng y = x giữ lại phần bên phải trục tung.
PT
1
CM
14 tháng 1 2017
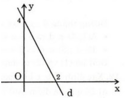
Hàm số y = 4 – 2x có:
+ Tập xác định D = R
+ Có a = –2 < 0 nên hàm số nghịch biến trên R.
+ Tại x = 0 thì y = 4 ⇒ A(0 ; 4) thuộc đồ thị hàm số.
Tại x = 2 thì y = 0 ⇒ B(2; 0) thuộc đồ thị hàm số.
Vậy đồ thị hàm số là đường thẳng đi qua hai điểm A(0 ; 4) và B(2; 0).
DT
0
PT
1
CM
12 tháng 8 2018
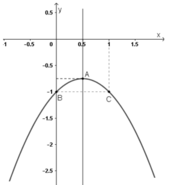
y = –x2 + x – 1
+ Tập xác định R
+ Đỉnh A(1/2 ; –3/4).
+ Trục đối xứng x = 1/2.
+ Đồ thị không giao với trục hoành.
+ Giao điểm với trục tung: B(0; –1).
Điểm đối xứng với B(0 ; –1) qua đường thẳng x = 1/2 là C(1 ; –1).
+ Bảng biến thiên:
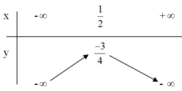
+ Đồ thị hàm số :
PT
1
CM
11 tháng 7 2019
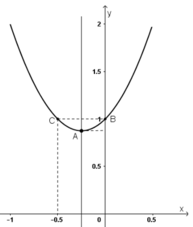
y = 2x2 + x + 1
+ Tập xác định: R
+ Đỉnh A(–1/4 ; 7/8).
+ Trục đối xứng x = –1/4.
+ Đồ thị không giao với trục hoành.
+ Giao điểm với trục tung B(0; 1).
Điểm đối xứng với B(0 ; 1) qua đường thẳng x = –1/4 là C(–1/2 ; 1)
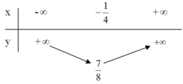
+ Bảng biến thiên:
+ Đồ thị hàm số:
PT
1
CM
5 tháng 11 2018
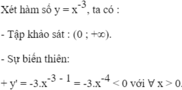
Do đó, hàm số đã cho nghịch biến trên tập xác định.
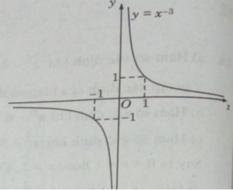
+ Giới hạn:
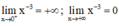
⇒ x = 0 (trục Oy) là tiệm cận đứng của đồ thị hàm số
y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên:
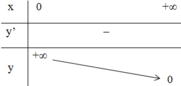
- Đồ thị:
PT
1
CM
22 tháng 3 2017
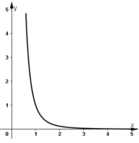
Tập xác định: R\{0}
Hàm số đã cho là hàm số lẻ.
Ta có: y′ < 0, ∀ x ∈ R \ {0} nên hàm số luôn nghịch biến trên các khoảng xác định.
Đồ thị có tiệm cận ngang là trục hoành, tiệm cận đứng là trục tung.
Bảng biến thiên:
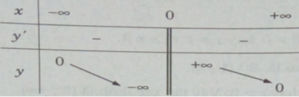
Đồ thị của hàm số có tâm đối xứng là gốc tọa độ.
PT
1
CM
6 tháng 12 2017
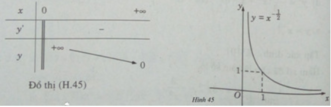
Tập xác định: D = (0; + ∞ )
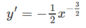
Vì y' < 0 ∀ x ∈ D nên hàm số nghịch biến.
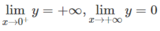
Đồ thị có tiệm cận đứng là trục tung, tiệm cận ngang là trục hoành.
Bảng biến thiên:
Hàm số y = |x + 1|
Nếu x + 1 ≥ 0 hay x ≥ –1 thì y = x + 1.
Nếu x + 1 < 0 hay x < –1 thì y = –(x + 1) = –x – 1.
+ Tập xác định: R
+ Trên (–∞; –1), y = x + 1 đồng biến.
Trên (–1 ; +∞), y = –x – 1 nghịch biến.
Ta có bảng biến thiên :
+ Đồ thị hàm số gồm hai phần:
Phần thứ nhất : Nửa đường thẳng y = x + 1 giữ lại các điểm có hoành độ ≥ –1.
Phần thứ hai : nửa đường thẳng y = –x – 1 giữ lại các điểm có hoành độ < –1.