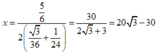Người ta cắt đôi đoạn dây thép dài 10m thành hai phần. Phần 1 lại cắt thành 6 phần bằng nhau và ghép thành một hình tứ diện, phần 2 lại cắt thành 12 phần bằng nhau và ghép thành một hình lập phương sao cho tổng diện tích xung quanh của hai hình là nhỏ nhất.
Gọi a là độ dài cạnh của hình tứ diện, b là độ dài cạnh của hình lập phương thì a + b là:
A . 5 + 5 3 3
B . - 5 + 5 3 3
C . - 5 + 20 3 6
D . 5 + 20 3 6



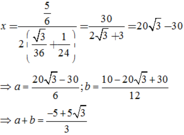

Đáp án C.
Gọi x là chiều dài đoạn thép thứ nhất, 0 < x < 10
=> Cạnh hình tứ diện là (tứ diện là đều)
Cạnh hình lập phương là 10 - x 12
Diện tích xung quanh của tứ diện là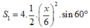
Diện tích xung quanh của lập phương là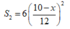
Tổng S 1 + S 2 đạt giá trị nhỏ nhất khi