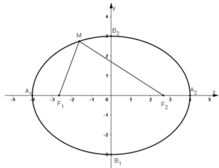
Biết Elip (E) có các tiêu điểm F 1 ( - 7 ; 0 ) , F 2 ( 7 ; 0 ) và đi qua M - 7 ; 9 4 Gọi N là điểm đối xứng với M qua gốc toạ độ. Chọn khẳng định đúng?
A. x 2 16 + y 2 12 = 1
B . M( 2;3)
C. F1( -2;0) và F2( 2;0)
D.NF1+ MF1= 8.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) (E): 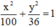 có a = 10; b = 6 ⇒ c2 = a2 – b2 = 64 ⇒ c = 8.
có a = 10; b = 6 ⇒ c2 = a2 – b2 = 64 ⇒ c = 8.
+ Tọa độ các đỉnh của elip là: A1(-10; 0); A2(10; 0); B1(0; -6); B2(0; 6)
+ Tọa độ hai tiêu điểm của elip: F1(-8; 0) và F2(8; 0)
+ Vẽ elip:
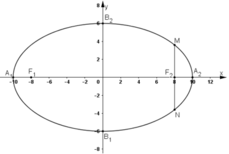
b) Ta có: M ∈ (E) ⇒ MF1 + MF2 = 2a = 20 (1)
MN // Oy ⇒ MN ⊥ F1F2 ⇒ MF12 – MF22 = F1F22 = (2c)2 = 162
⇒ (MF1 + MF2).(MF1 – MF2) = 162
⇒ MF1 – MF2 = 12,8 (Vì MF1 + MF2 = 20) (2).
Từ (1) và (2) ta có hệ phương trình
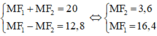
Vậy MN = 2.MF2 = 7,2.

Elip (E): 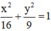 có a = 4, b = 3 ⇒ c2 = a2 – b2 = 7 ⇒ c = √7.
có a = 4, b = 3 ⇒ c2 = a2 – b2 = 7 ⇒ c = √7.
+ Các đỉnh của elip là: A1(–4; 0); A2(4; 0); B1(0; –3); B2(0; 3).
+ Tiêu điểm của elip: F1(–√7; 0); F2(√7; 0).
+ Vẽ elip:

Ta có a2= 16 và b2= 12 nên c2= 16-12= 4
=> 2 tiêu cự là F1( -2;0) và F2( 2;0)
Điểm M thuộc (E) và
![]()
Từ đó
![]()
Chọn C

Đáp án D
Phương trình chính tắc của elip có dạng:
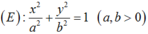
Theo giải thiết ta có c = 4
Chu vi của tam giác MF1F2 bằng 18 nên
MF1+ MF2+ F1F2 = 2a+ 2c nên 2a+ 2c= 18
Mà c= 4 => a= 5


Chọn đáp án D

MEMORIZE |
Định nghĩa đường elip, phương trình chính tắc của elip. |
Đáp án D
Do N đối xứng với M qua gốc tọa độ nên tọa độ điểm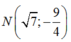
Suy ra:
Từ đó: NF1+ MF1= 8.