Cho α là góc tạo bởi hai đường thẳng d 1 : 2 x − 3 y + 4 = 0 v à d 2 : 3 x + y = 0 . Khẳng định nào sau đây là đúng?
A. cos α = 3 130
B. sin α = 3 130
C. cos α = − 3 130
D. sin α = − 3 130
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐÁP ÁN B
Đường thẳng d1 có VTPT n 1 → ( 1 ; 3 )
Đường thẳng d2 có VTPT n 2 → ( 2 ; − 1 )
Cosin góc giữa hai đường thẳng đã cho là:
cos α = 1.2 + 3. ( − 1 ) 1 2 + 3 2 . 2 2 + ( − 1 ) 2 = 1 5 2
Lại có; sin 2 α + c os 2 α = 1 ⇔ sin 2 α = 1 − c os 2 α = 1 − 1 50 = 49 50
Do 0 0 < α < 90 0 ⇒ sin α > 0 ⇒ sin α = 7 5 2

Đáp án C
Cho đường thẳng d có phương trình y = ax + b (a ≠ 0)
Gọi α là góc tạo bởi tia Ox và d . Ta có: α = tan α

Đáp án C
Cho đường thẳng d có phương trình y = ax + b (a ≠ 0)
Gọi α là góc tạo bởi tia Ox và d . Ta có: α = tan α

Chọn C.
Các đường phân giác của các góc tạo bởi d và d' có phương trình:
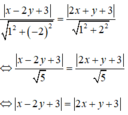
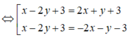
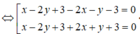
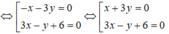
ĐÁP ÁN A
Đường thẳng d1 có VTPT n 1 → ( 2 ; − 3 )
Đường thẳng d2 có VTPT n 2 → ( 3 ; 1 )
Cosin góc giữa hai đường thẳng đã cho là:
cos α = 2.3 + ( − 3 ) .1 2 2 + ( − 3 ) 2 . 3 2 + 1 2 = 3 130