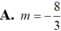
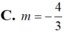
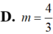
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Để 2 đường thẳng đã cho trùng nhau khi và chỉ khi:
Hệ phương trình
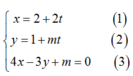có vô số nghiệm.
Thay (1) ; (2) vào (3) ta được : 4 (2+ 2t) -3 (1+ mt) + m= 0
Hay ( 3m- 8)t = m+5 (*)
Phương trình (*) có vô số nghiệm khi và chỉ khi
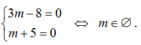
Bài 1)
a) Xét phương trình hoành độ giao điểm: \(2x+3+m=3x+5-m\)
\(\Leftrightarrow x=3+m+m-5\Leftrightarrow x=2m-2\)
Để giao điểm của hai đường thẳng trên nằm trên trục tung thì \(2m-2=0\Leftrightarrow m=1\)
b) Do (d) // (d') nên (d) có phương trình \(y=-\frac{1}{2}x+b\)
Do (d) cắt trục hoành tại điểm có hoành độ x = 10 nên điểm (10;0) thuộc đường thẳng (d0.
Vậy thì \(0=-\frac{1}{2}.10+b\Leftrightarrow b=5\)
Vậy phương trình đường thẳng (d) là \(y=-\frac{1}{2}x+5\)
Bài 2)
a) Để (d1)//(d2) thì \(4m=3m+1\Leftrightarrow m=1\)
b) Để (d1)//(d2) thì \(4m\ne3m+1\Leftrightarrow m\ne1\)
Khi m = 2, ta có phương trình hoành độ giao điểm là:
\(8x-7=7x-7\Leftrightarrow x=0\)
Với \(x=0,y=-7\)
Vậy tọa độ giao điểm của (d1) và (d2) là (0; -7)
Để hai đường thẳng song song mà không trùng nhau thì điều kiện cần và đủ là :
\(\hept{\begin{cases}m=1\\3m+2\ne1\end{cases}\Leftrightarrow\hept{\begin{cases}m=1\\m\ne-\frac{1}{3}\end{cases}\Leftrightarrow}m=1}\)
Để 3 đường thẳng trên là ba đường thẳng phân biệt thì m + 2 ≠ 1 m ≠ 1 m ≠ m + 2 ⇔ m ≠ 1 m ≠ − 1
Xét phương trình hoành độ giao điểm của d 2 v à d 3 :
x + 2 = m x + 2 ⇔ x ( m – 1 ) = 0 x = 0 m = 1 ( k t m )
Với x = 0 y = 2 nên giao điểm của d 2 ; d 3 là M (0; 2)
Để ba đường thẳng trên giao nhau tại 1 điểm thì M ∈ d 1 nên:
2 = ( m + 2 ) . 0 – 3 m – 3 ⇔ 3 m = − 5 ⇔ m = − 5 3 ( t m )
Vậy m = − 5 3
Đáp án cần chọn là: B
Thay (1) ; (2) vào (3) ta được 4( 1+ 2t) -3( 4+ mt) + 3m = 0
Hay ( 3m- 8) t= 3m- 8 (*)
Phương trình (*) có nghiệm tùy ý khi và chỉ khi 3m- 8= 0 hay m= 8/3.
Chọn B.