Cho hệ phương trình x + 2 y = 2 m x − y = m . Trong trường hợp hệ phương trình có nghiệm duy nhất (x; y), tìm điều kiện của m để x > 1 và y > 0
A. m > 0
B. m > 1
C. m < −1
D. m > 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(\left\{{}\begin{matrix}m^2x-my=2m\\x+my=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m^2+1\right)x=2m+1\\y=\dfrac{1-x}{m}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m+1}{m^2+1}\\y=\dfrac{1-\dfrac{2m+1}{m^2+1}}{m}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m+1}{m^2+1}\\y=\dfrac{\dfrac{m^2+1-2m-1}{m^2+1}}{m}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m+1}{m^2+1}\\y=\dfrac{\dfrac{m^2-2m}{m^2+1}}{m}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m+1}{m^2}\\y=\dfrac{m^2-2m}{m^2+1}:m=\dfrac{m\left(m-2\right)}{m\left(m^2+1\right)}=\dfrac{m-2}{m^2+1}\end{matrix}\right.\)
b, Để hpt có nghiệm duy nhất khi \(\dfrac{m}{1}\ne-\dfrac{1}{m}\Leftrightarrow m^2\ne-1\left(luondung\right)\)
\(\dfrac{2m+1}{m^2}+\dfrac{m-2}{m^2+1}=-1\)
\(\Leftrightarrow\left(2m+1\right)\left(m^2+1\right)+m^2\left(m-2\right)=-m^2\left(m^2+1\right)\)
\(\Leftrightarrow2m^3+2m+m^2+1+m^3-2m^2=-m^4-m^2\)
\(\Leftrightarrow3m^3-m^2+2m+1=-m^4-m^2\)
\(\Leftrightarrow m^4+3m^3+2m+1=0\)
bạn tự giải nhé

Ta có
m x − y = 2 m 4 x − m y = m + 6 ⇔ y = m x − 2 m 4 x − m m x − 2 m = m + 6 ⇔ y = m x − 2 m x m 2 − 4 = 2 m 2 − m − 6
Hệ phương trình có nghiệm duy nhất khi m 2 − 4 ≠ 0 ⇔ m ≠ 2 ; − 2
Khi đó x = 2 m 2 − m − 6 m 2 − 4 = 2 m + 3 m − 2 m − 2 m + 2 = 2 m + 3 m + 2
⇒ y = m . 2 m + 3 m + 2 − 2 m = − m m + 2 ⇒ x = 2 m + 3 m + 2 y = − m m + 2 ⇔ x = 2 − 1 m + 2 y = − 1 + 2 m + 2 ⇔ 2 x = 4 − 2 m + 2 y = − 1 + 2 m + 2 ⇒ 2 x + y = 3
vậy hệ thức không phụ thuộc vào m là 2x + y = 3
Đáp án: D

m x − y = m 2 2 x + m y = − m 3 + 2 m + 2 ⇔ y = m x − m 2 2 x + m m x − m 2 = − m 3 + 2 m + 2 ⇔ y = m x − m 2 x m 2 + 2 = 2 m + 2 ⇔ x = 2 m + 2 m 2 + 2 y = m . 2 m + 2 m 2 + 2 − m 2 ⇔ x = 2 m + 2 m 2 + 2 y = − m 4 + 2 m m 2 + 2
(vì m 2 + 2 > 0 ; ∀ m )
Suy ra x – y = m 4 + 2 m 2 + 2
Đáp án: C

Ta có m x − y = 2 m 4 x − m y = m + 6
⇔ y = m x − 2 m 4 x − m m x − 2 m = m + 6 ⇔ y = m x − 2 m x m 2 − 4 = 2 m 2 − m − 6
Hệ phương trình có nghiệm duy nhất khi m 2 – 4 ≠ 0 ⇔ m ≠ {−2; 2}
Khi đó x = 2 m 2 − m − 6 m 2 − 4 = 2 m + 3 m − 2 m + 2 m − 2 = 2 m + 3 m + 2
⇒ y = m . 2 m + 3 m + 2 − 2 m = − m m + 2
Thay x = 2 m + 3 m + 2 y = − m m + 2 vào phương trình 6x – 2y = 13 ta được
6. 2 m + 3 m + 2 − 2. − m m + 2 = 13 ⇔ 14 m + 18 m + 2 = 13
⇔ 14m + 18 = 13m + 26
m = 8 (TM)
Vậy m = 8 là giá trị cần tìm
Đáp án: C

Đáp án C
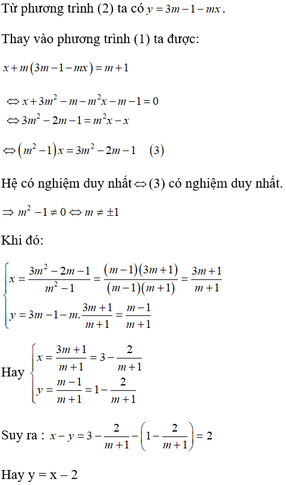
Vậy điểm M(x; y) luôn chạy trên đường thẳng cố định có phương trình y = x - 2

a) Với m = -2
=> hpt trở thành: \(\left\{{}\begin{matrix}x+y=2\\-2x-y=-2\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}y=2-x\\-x=0\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\)
Vậy S = {0; 2}
b) Ta có: \(\left\{{}\begin{matrix}x+y=2\left(1\right)\\mx-y=m\left(2\right)\end{matrix}\right.\)
=> x + mx = 2 + m
<=> x(m + 1) = 2 + m
Để hpt có nghiệm duy nhất <=> \(m\ne-1\)
<=> x = \(\dfrac{m+2}{m+1}\) thay vào pt (1)
=> y = \(2-\dfrac{m+2}{m+1}=\dfrac{2m+2-m-2}{m+1}=\dfrac{m}{m+1}\)
Mà 3x - y = -10
=> \(3\cdot\dfrac{m+2}{m+1}-\dfrac{m}{m+1}=-10\)
<=> \(\dfrac{2m+6}{m+1}=-10\) <=> m + 3 = -5(m + 1)
<=> 6m = -8
<=> m = -4/3
c) Để hpt có nghiệm <=> m \(\ne\)-1
Do x;y \(\in\) Z <=> \(\left\{{}\begin{matrix}\dfrac{m+2}{m+1}\in Z\\\dfrac{m}{m+1}\in Z\end{matrix}\right.\)
Ta có: \(x=\dfrac{m+2}{m+1}=1+\dfrac{1}{m+1}\)
Để x nguyên <=> 1 \(⋮\)m + 1
<=> m +1 \(\in\)Ư(1) = {1; -1}
<=> m \(\in\) {0; -2}
Thay vào y :
với m = 0 => y = \(\dfrac{0}{0+1}=0\)(tm)
m = -2 => y = \(\dfrac{-2}{-2+1}=2\)(tm)
Vậy ....

Từ phương trình (1) ta có x = 2y + 5. Thay x = 2y + 5 vào phương trình (2) ta được: m(2y + 5) – y = 4 ⇔ (2m – 1).y = 4 – 5m (3)
Hệ có nghiệm duy nhất khi và chỉ khi (3) có nghiệm duy nhất. Điều này tương đương với 2m – 1 ≠ 0 ⇔ m ≠ 1 2
Từ đó ta được: y = 4 − 5 m 2 m − 1 và x = 5 + 2 y = 3 2 m − 1 . Ta có:
x . y = 3 4 − 5 m 2 m − 1 2 . Do đó x. y < 0 4 – 5m < 0 ⇔ m > 4 5 (thỏa mãn điều kiện)
Đáp án:A
Ta có x + 2 y = 2 m x − y = m
⇔ x = 2 − 2 y m 2 − 2 y − y = m ⇔ x = 2 − 2 y 2 m + 1 y = m
Để phương trình có nghiệm duy nhất thì m ≠ - 1 2
Suy ra y = m 2 m + 1 ⇒ x = 2 − 2. m 2 m + 1 ⇒ x = 2 m + 2 2 m + 1
Vậy hệ có nghiệm duy nhất x = 2 m + 2 2 m + 1 y = m 2 m + 1
Để x > 1 y > 0
⇔ 2 m + 2 2 m + 1 > 1 m 2 m + 1 > 0 ⇔ 1 2 m + 1 > 0 m 2 m + 1 > 0 ⇔ 2 m + 1 > 0 m > 0 ⇔ m > − 1 2 m > 0 ⇒ m > 0
Kết hợp điều kiện m ≠ - 1 2 ta có m > 0
Đáp án: A