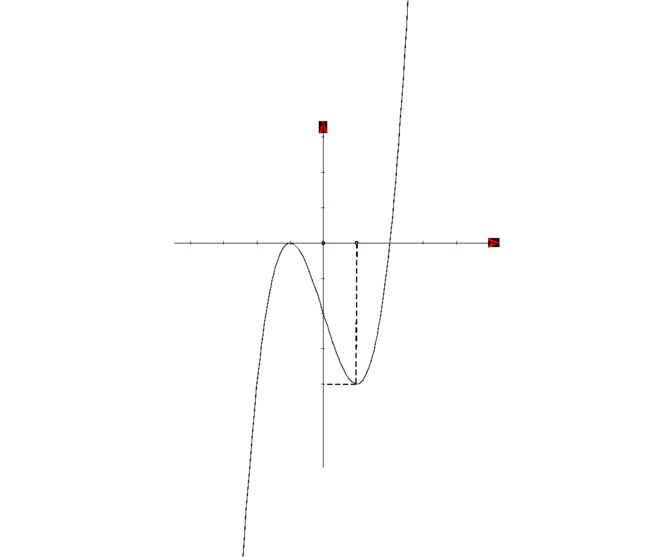
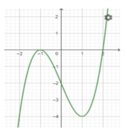
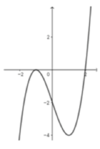
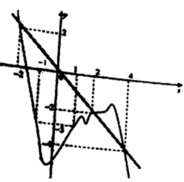
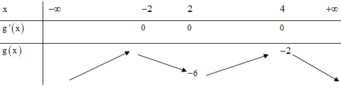
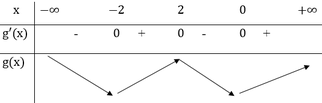
Cho hàm số y = f(x) có đồ thị hàm số y = f '(x) như hình vẽ. Xét hàm số
g
x
=
2
f
x
+
2
x
3
-
4
x
-
3
m
-
6
5
với m là số thực. Để
g
x
≤
0
,
∀
x
∈
-
5
;
5
thì điều kiện của m là A.
m
≥
2
3
f
5
B.
m
≤
2
3
f
5
C.
m
...
Đọc tiếp
Cho hàm số y = f(x) có đồ thị hàm số y = f '(x) như hình vẽ. Xét hàm số g x = 2 f x + 2 x 3 - 4 x - 3 m - 6 5 với m là số thực. Để g x ≤ 0 , ∀ x ∈ - 5 ; 5 thì điều kiện của m là
A. m ≥ 2 3 f 5
B. m ≤ 2 3 f 5
C. m ≤ 2 3 f 0 - 2 5
D. m ≥ 2 3 f - 5 - 4 5
đạt cực trị tại 
.
nghịch biến trên 
. 
đồng biến trên 
.
đồng biến trên 
.
=> 
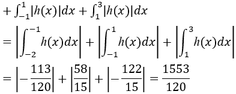
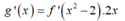
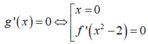
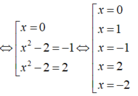
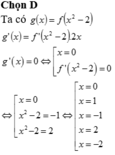
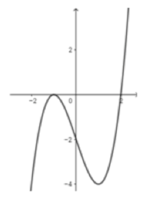
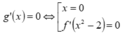
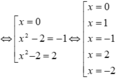
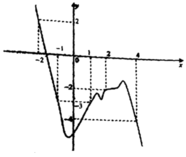
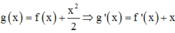
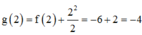
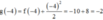
Đáp án A
Ta có g x = 2 f x + 2 x 3 - 4 x - 3 m - 6 5 ≤ 0 , ∀ x ∈ - 5 ; 5
⇔ h x = 2 f x + 2 x 3 - 4 x - 6 5 ≤ 3 m , ∀ x ∈ - 5 ; 5 ⇔ m a x - 5 ; 5 h x ≤ 3 m
Mặt khác h ' x = 2 f ' x + 6 x 2 - 4 = 0 ⇔ f ' x = 2 - 3 x 2
Dựa vào đồ thị f '(x) ta thấy rằng phương trình f ' x ≥ 2 - 3 x 2 , ∀ x ∈ - 5 ; 5
Do đó h(x) đồng biến trên đoạn - 5 ; 5
Suy ra h 5 = 2 f 5 ≤ 3 m ⇔ m ≥ 2 3 f 5 .