Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính A B = 2 a , S A = a 3 và vuông góc với mặt phẳng ABCD. Cosin của góc giữa hai mặt phẳng S A D và S B C bằng
A. 2 2
B. 2 3
C. 2 4
D. 2 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
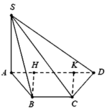
Gọi H, K lần lượt là hình chiếu của B, C trên AD
Gọi α là góc giữa 2 mặt phẳng S A D , S B C
⇒ Δ S H K là hình chiếu của Δ S B C trên S A D ⇒ c o s α = S S H K S S B C
Ta có H K = B C = 2 a ⇒ S S H K = 1 2 S A . H K = a 3 .2 a 2 = a 2 3
Lại có d A ; B C = B H = a 3 ⇒ d S ; B C = a 3 . 2 = a 6
Suy ra S S B C = 1 2 d S ; B C . B C = a 3 6 .
Vậy c o s α = a 3 3 a 3 6 = 2 2

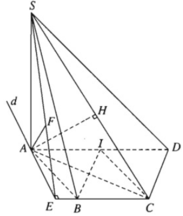
a) Vì ABCD là nửa lục giác đều nội tiếp trong đường tròn đường kính AD = 2a nên ta có: AD //BC và AB = BC = CD = a, đồng thời AC ⊥ CD, AB ⊥ BD, AC = BD = a√3.
Như vậy 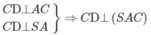
Trong mặt phẳng (SAC) dựng AH ⊥ SC tại H ta có AH ⊥ CD và AH ⊥ SC nên AH ⊥ (SCD)
Vậy AH = d(A,(SCD))
Xét tam giác SAC vuông tại A có AH là đường cao, ta có:
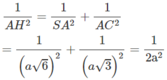
Vậy A H 2 = 2 a 2 ⇒ A H = a 2
Gọi I là trung điểm của AD ta có BI // CD nên BI song song với mặt phẳng (SCD). Từ đó suy ra d(B, (SCD)) = d(I,(SCD)).
Mặt khác AI cắt (SCD) tại D nên
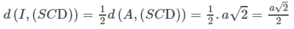
Do đó: 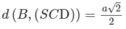
b) Vì AD // BC nên AD // (SBC), do đó d(AD, (SBC)) = d(A,(SBC))
Dựng AD ⊥ BC tại E ⇒ BC ⊥ (SAE)
Dựng AD ⊥ SE tại F ta có:
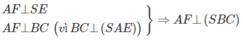
Vậy AF = d(A,(SBC)) = d(AD, (SBC))
Xét tam giác vuông AEB ta có:
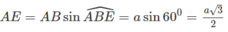
Xét tam giác SAE vuông tại A ta có:
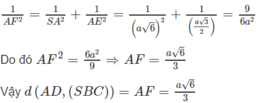

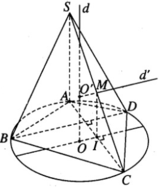
Trong mặt phẳng chứa đường tròn tâm O ngoại tiếp tứ giác ABCD ta kẻ đường kính qua O vuông góc với dây cung AC tại I. Ta có IA = IC và OI // BD. Gọi O’ là tâm mặt cầu đi qua 5 đỉnh của hình chóp. Khi đó điểm O’ phải nằm trên trục d của đường tròn ngoại tiếp tứ giác ABCD. Ta có d ⊥ (ABCD) tại O. Gọi M là trung điểm của cạnh SC. Ta có MI // SA nên MI ⊥ (ABCD) tại I. Từ M kẻ đường thẳng d’ // OI cắt d tại O’. Vì d′ ⊥ (SAC) tại M nên ta có O’C = O’S và O’C là bán kính r của mặt cầu ngoại tiếp hình chóp S.ABCD
Ta có:
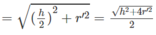

Vì SA không đổi nên ta có V SABCD lớn nhất khi và chỉ khi S ABCD lớn nhất. Ta có S ABCD = AC.BD/2 trong đó AC và BD là hai dây cung vuông góc với nhau. Vậy AC.BD lớn nhất khi và chỉ khi AC = BD = 2r’, nghĩa là tứ giác ABCD là một hình vuông.

Chọn C
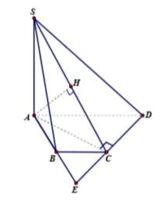
Từ giả thiết ta có AB=BC=CD=a
Kẻ AH ⊥ SC
Do AD là đường kính nên AC ⊥ CD và A C = A D 2 - C D 2 = a 3
Do SA ⊥ CD, AC ⊥ CD => CD ⊥ (SAC)=> CD ⊥ AH
=>AH ⊥ SC, AH ⊥ CD => AH ⊥ (SCD)
⇒ d A ( S C D ) = A H = A S . A C A S 2 + A C 2 = a 6 . a 3 3 a = a 2
Kéo dài AB cắt CD tại E. Dễ thấy B là trung điểm của AE.
⇒ d B , S C D d ( A , S C D ) = B E A E = 1 2 ⇒ d B , ( S C D ) = a 2 2