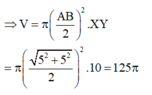Bên trong hình vuông cạnh a, dựng hình sao bốn cánh đều như hình vẽ bên (các kích thước cần thiết cho như ở trong hình).
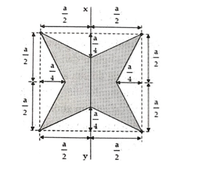
Tính thể tích của khối tròn xoay sinh ra khi quay hình sao đó quanh trục Oy
A. 5π/48 a 3
B. 5π/16 a 3
C. π/6 a 3
D.π/8 a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
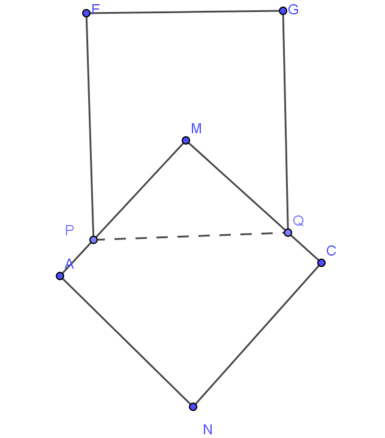
Gọi V 1 là thể tích khối trong xoay khi xoay hình vuông EGQP quanh MN. Khối này có bán kính đáy R = 1 2 E G = 5 2 và đường cao = EP = 5 => V 1 = 5 . 5 2 2 π = 125 4 π
Gọi V 2 là thể tích khối tròn xoay khi xoay hình vuông AMCN quanh MN, khối này là hợp lại của 2 khối nón đêu có bán kính đáy R = 1 2 A C = 5 2 2 Đường cao h = 1 2 M N = 5 2 2 => V 2 = 2 . 1 3 . 5 2 2 . 5 2 2 2 π = 125 2 6 π
Gọi V 3 là thể tích của khối nón tròn xoay khi quay MPQ quanh MN, khối này óc bán kính đáy R = 1 2 P Q = 5 2 đường cao h = d ( M ; P Q ) = 5 2 => V 3 = 1 3 . 5 2 . 5 2 2 . π = 125 12 π
Ta có thể tích của toàn khối tròn xoay V = V 1 + V 2 - V 3 = 125 1 + 2 π 6

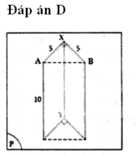
Khi quay mặt phẳng (P) xung quanh trục XY thì vật thể tròn xoay sinh ra bởi hình (H) là phần in đậm như hình bên. Nhìn hình ta thấy thể tích V cần tim bằng thể tích của hình trụ có đường kính đáy bằng AB và chiều cao bằng XY