Cho tứ diện đều ABCD. Biết khoảng cách từ điểm A đến mặt phẳng (BCD) bằng 6. Tính thể tích của tứ diện ABCD
A. V = 27 3
B. V = 5 3
C. V = 27 3 2
D. V = 9 3 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 8 2019
Đáp án B
Gọi O là tâm của tam giác BCD và M là trung điểm CD
⇒
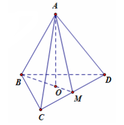A
O
⊥
(
B
C
D
)
⇒
d
A
;
B
C
D
=
A
O
=
6
Đặt độ dài cạnh của tứ diện ABCD là x ⇒ B O = 2 B M 3 = x 3 3
⇒ A O = A B 2 - B O 2 = x 6 3 = 6 ⇔ x = 3 6
⇒ V = S B C D . A O 3 = x 2 3 . A O 12 = 27 3
CM
21 tháng 6 2017
Đáp án A
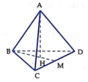
Gọi H là hình chiếu của điểm A trên mặt phẳng (BCD). Do ABCD là tứ diện đều nên tâm H là tâm đường trong ngoại tiếp ∆ BCD.
Đặt cạnh của tứ diện là a. Gọi M là trung điểm của CD.
Do ∆ BCD đều nên
Ta có ∆ ABH vuông tại H nên
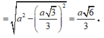
Từ giả thiết ta có
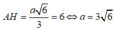
Vậy thể tích của tứ diện ABCD là
CM
28 tháng 8 2019
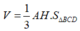
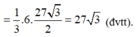
Đáp án A
Gọi G là trọng tâm tam giác đều ABC suy ra G A ⊥ ( B C D )
Gọi M là trung điểm BD.
Đặt A C = x ⇒ G C = 2 3 C M = x 3 3
lại có A C 2 - G C 2 = A G 2
⇒ x = a 6 2
Đáp án A
Gọi H là hình chiếu của điểm A trên mặt phẳng(BCD). Do ABCD là tứ diện đều nên tâm H là tâm đường trong ngoại tiếp Δ B C D .
Đặt cạnh của tứ diện là a. Gọi M là trung điểm của CD.
Do Δ B C D đều nên
B M = a 3 2 ⇒ B H = 2 3 B M = 2 3 . a 3 2 = a 3 3
Ta có Δ A B H vuông tại H nên
A H = A B 2 − B H 2 = a 2 − a 3 3 2 = a 6 3
Từ giả thiết ta có
A H = a 6 3 = 6 ⇔ a = 3 6 ⇒ S Δ B C D = a 2 3 4 = 27 3 2
(đvdt).
Vậy thể tích của tứ diện ABCD là
A H = a 6 3 = 6 ⇔ a = 3 6 ⇒ S Δ B C D = a 2 3 4 = 27 3 2
(đvtt).