Cho tam giác ABC vuông tại A. Gọi P, Q, R lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi O là giao điểm của ba đường phân giác. Khi đó, tâm đường trong ngoại tiếp tam giác ABC là điểm:
(A) O
(B) P;
(C) Q;
(D) R.
Hãy chọn phương án đúng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

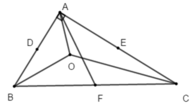
+ Vì O là giao điểm của ba đường phân giác trong tam giác ABC nên O là tâm của đường tròn nội tiếp tam giác ABC nên đáp án A sai.
+ Tam giác ABC vuông tại A có F là trung điểm của BC nên AF là đường trung tuyến ứng với cạnh huyền
Do đó: AF = 1 2 BC (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Suy ra AF = FC = FB
Nên F cách đều ba đỉnh A, B, C
Do đó F là tâm đường tròn ngoại tiếp tam giác ABC.
+ Vì D ≠ E ≠ F và chỉ có một đường tròn ngoại tiếp tam giác ABC nên đáp án B, C sai và D đúng.
Chọn đáp án D

a, Vì HM là đường cao => \(HM\perp AB\)=> ^HMA = 900
Vì HN là đường cao => \(HN\perp AC\)=> ^HNA = 900
Xét tứ giác AMHN có :
^HMA + ^HNA = 900
mà ^HMA ; ^HNA đối nhau
Vậy tứ giác AMHN nội tiếp
b, Xét tam giác ABH vuông tại H, đường cao HM ta có :
\(AH^2=AM.AB\)(1)
Xét tam giác ACH vuông tại H, đường cao HN ta có :
\(AH^2=AN.AC\)(2)
từ (1) ; (2) suy ra : \(AM.AB=AN.AC\Rightarrow\frac{AM}{AC}=\frac{AN}{AB}\)
Xét tam giác AMN và tam giác ACB ta có :
^A chung
\(\frac{AM}{AC}=\frac{AN}{AB}\)( cmt )
Vậy tam giác AMN ~ tam giác ACB ( c.g.c )

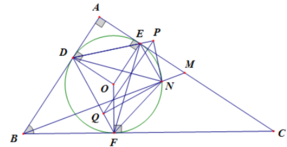
Vì DPN+DQN=90o+90o=180o nên DPNQ là tứ giác nội tiếp
=>QPN=QDN (hai góc nội tiếp cùng chắn cung QN) (5)
Mặt khác DENF là tứ giác nội tiếp nên QDN=FEN (6)
Từ (5) và (6) ta có FEN=QPN (7)
Tương tự ta có: EFN=PQN (8)
Từ (7) và (8) suy ra Δ N P Q ~ Δ N E F ( g . g ) = > P Q E F = N Q N F
Theo quan hệ đường vuông góc – đường xiên, ta có
N Q ≤ N F = > P Q E F = N Q N F ≤ 1 = > P Q ≤ E F
Dấu bằng xảy ra khi Q ≡ F ⇔ NF ⊥ DF ⇔ D, O, N thẳng hàng.
Do đó PQ max khi M là giao điểm của AC và BN, với N là điểm đối xứng với D qua O.

a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét ΔABC có
BE là đường cao
CF là đường cao
BE cắt CF tại H
Do đó: AH⊥BC
hay AF⊥BC
Chọn đáp án D