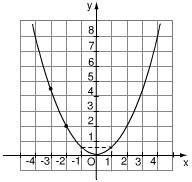
Biết rằng đường cong trong hình 11 là một parapol y = ax2.
Tìm tung độ của điểm thuộc parapol có hoành độ x = -3.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 11 2019
a) Ta có đồ thị hàm số y = ax2 đi qua điểm (-2 ; 2)
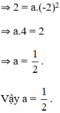
b) Tại x = -3 ta có: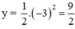 
Vậy điểm có hoành độ x = -3 thì tung độ bằng 4,5.
c) Hoành độ các điểm có tung độ y =8 thỏa mãn phương trình: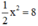 
⇔ x2 = 16 ⇔ x = 4 hoặc x = -4.
Vậy các điểm thuộc parabol có tung độ bằng 8 là (4; 8) và (-4; 8).
CM
6 tháng 6 2018
Hoành độ các điểm có tung độ y =8 thỏa mãn phương trình: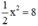 
⇔ x2 = 16 ⇔ x = 4 hoặc x = -4.
Vậy các điểm thuộc parabol có tung độ bằng 8 là (4; 8) và (-4; 8).
PT
1
4 tháng 4 2017
Bài giải:
a) Theo hình vẽ, ta lấy điểm A thuộc đồ thị có tọa độ là x = -2, y = 2. Khi đó ta được:
2 = a . (-2)2 suy ra a = 
b) Đồ thị có hàm số là y = x2 . Tung độ của điểm thuộc parabol có hoành độ x = -3 là y = (-3)2 suy ra y = 
.
c) Các điểm thuộc parabol có tung độ là 8 là:
8 = x2 ⇔ x2 = 16 ⇔ x = ± 4
Ta được hai điểm và tọa độ của hai điểm đó là M(4; 8) và M'(-4; 8).
23 tháng 1 2019
a, bảng giá trị tương ứng của x và y
| x | -2 | -1 | 0 | 1 | 2 |
| y | -4 | -1 | 0 | -1 | -4 |
b, Vì (d) có hệ số góc bằng 3 nên (d) có dạng y = 3x + b
Vì M(2;yM) thuộc (P) nên \(y_M=-2^2=-4\)
=> M(2 ; -4)
Vì M thuộc (d) nên
-4 = 3.2 + b
=> b = -10
=> (d) y = 3x - 10
PK
1
H
28 tháng 5 2023
Phương trình hoành độ giao điểm: \(x^2=3\left(2m+3\right)-2mx=0\Leftrightarrow x^2+2mx-3\left(2m+3\right)=0\)
Để (d) cắt (P) tại hai điểm có hoành độ cùng dấu .
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\3\left(2m+3\right)>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left(m+3\right)^2>0\\6m+9>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne3\\m< -\dfrac{3}{2}\end{matrix}\right.\)
Vậy \(m\ne3,m< -\dfrac{3}{2}\) là giá trị m cần tìm.
Tại x = -3 ta có: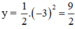
Vậy điểm có hoành độ x = -3 thì tung độ bằng 4,5.