Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án: B
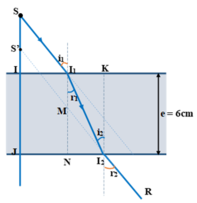
Ta thấy tia ló I 2 R song song với tia tới S I 1 , giao của đường kéo dài của tia I 2 R cắt tia sáng SJ tại S’, S’ là ảnh của S qua bản mặt.
Tứ giác S S ' M I 1 là hình bình hành
→ S S ' = I 1 M
Xét 2 tam giác vuông M N I 2 và I 1 N I 2 ta có:
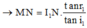
Vì ta đang xét góc tới i 1 rất nhỏ nên r 1 cũng rất nhỏ
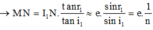
(theo định luật khúc xạ tại I 1 : sin i 1 = n . sin r 1 )
→Khoảng cách giữa vật và ảnh là:
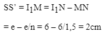
Đáp án: C
Tương tự câu 12
Ảnh S’ cách bản mặt trên một đoạn:
S’I = SI – S’S = 20 - 2 = 18cm.
Đáp án C
Ảnh S’ cách bản mặt trên một đoạn
S’I = SI – S’S = 20 - 2 = 18cm
Chọn C
Hướng dẫn: Áp dụng công thức ảnh của một điểm sáng qua bản hai mặt song song khi ánh sáng truyền gần như vuông góc với bề mặt của hai bản SS’ = e 1 − 1 n
Chọn B
Hướng dẫn: Áp dụng công thức ảnh của một điểm sáng qua bản hai mặt song song khi ánh sáng truyền gần như vuông góc với bề mặt của hai bản SS’ = e 1 − 1 n
Chọn đáp án C.
Nếu không có bản mặt song song, ảnh A 1 B 1 đối xứng với AB qua gương nên A 1 B 1 cách AB một khoảng 72cm.
Khi có bản mặt song song, mỗi lần qua bản mặt song song tia sáng dịch theoc hiều truyền ánh sáng một đoạn:
Vì hai lần tia sáng đi qua nên ảnh A 1 B 1 dịch đến A 2 B 2 một đoạn 2ΔS = 4cm, tức là cách AB một đoạn: 72 – 4 = 68cm
Vì khá lười vẽ hình nên mình sẽ lấy hình trên Internet nhé
Ta có: \(SS'=IM=e-MK\)
\(i=\widehat{IMS'}=\widehat{KMJ}\Rightarrow\tan i=\dfrac{KJ}{MK}\Rightarrow MK=\dfrac{KJ}{\tan i}\)
\(r=\widehat{I'JI}\Rightarrow\tan r=\dfrac{II'}{e}=\dfrac{KJ}{e}\)
\(\Rightarrow SS'=e-\dfrac{e\tan r}{\tan i}=e\left(1-\dfrac{\tan r}{\tan i}\right)\sim e\left(1-\dfrac{r}{i}\right)\)
\(i=n.r\Rightarrow SS'=6\left(1-\dfrac{1}{n}\right)=6\left(1-\dfrac{2}{3}\right)=2\left(cm\right)\)
\(\Rightarrow S'H=SH-SS'=20-2=18\left(cm\right)\)
Đáp án B