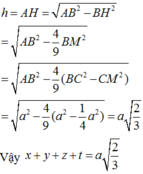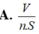
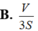
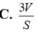
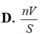
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Gọi O là một điểm bất kì bên trong khối đa diện.
Chia khối đa diện đều n mặt đã cho thành n khối chóp có đỉnh là O và các mặt đáy là các mặt của khối đa diện. Chiều cao hạ từ O đến n mặt tương ứng là h 1 , h 2 , . . . , h n
Khi đó
Đáp án D
Gọi O là một điểm bất kì bên trong khối đa diện.
Chia khối đa diện đều n mặt đã cho thành n khối chóp có đỉnh là O và các mặt đáy là các mặt của khối đa diện. Chiều cao hạ từ O đến n mặt tương ứng là
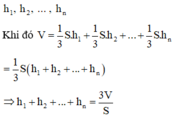
Đáp án A
Gọi O là một điểm bất kì bên trong khối đa diện.
Chia khối đa diện đều n mặt đã cho thành n khối chóp có đỉnh là O và các mặt đáy là các mặt của khối đa diện. Chiều cao hạ từ O đến n mặt tương ứng là h 1 , h 2 , . .. , h n n
Khi đó
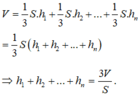
Chọn C
Vì bài toán cho với đa diện đều n mặt và một điểm bất kỳ bên trong đa diện, nên ta chọn đa diện đều là hình lập phương cạnh a, và điểm bất kỳ là tâm I của nó. Khi đó, ta có:
Tổng khoảng cách từ I đến các mặt bên là 6 × a 2 = 3 a (đvđd)
Thể tích V = a 3 (đvtt), diện tích mỗi mặt bên S = a 2 (đvdt)
Suy ra, tổng khoảng cách bằng 3 V S .
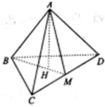
Chọn B.
Gọi x, y, z, t lần lượt là khoảng cách từ M đến các mặt phẳng (BCD), (CDA), (DAB), (ABC). Ta có
Cộng lại ta thu được (chú ý rằng)
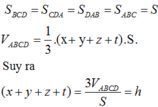
với h là độ dài đường cao của tứ diện đều ABCD. Ta có
