Cho (P) y = x 2 + 1 và đường thẳng d: mx-y+2=0. Tìm m để diện tích hình phẳng giới hạn bởi (P) và d đạt giá trị nhỏ nhất:
A. 0,5
B. 0,75
C. 1
D. 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 2 2019
Phương trình hoành độ giao điểm của (P) và d là x 2 - m x - 1 = 0
Ta có ∆ = m 2 + 4 > 0 ∀ m . Suy ra phương trình luôn có 2 nghiệm phân biệt x 1 ; x 2
Giả sử x 1 < x 2 . Khi đó:
S = ∫ x 1 x 2 m x + 2 - x 2 - 1 d x = ∫ x 1 x 2 m x + 1 - x 2 d x = m 2 + 4 m 2 6 + 2 3 ≥ 4 3
Vậy m i n S = 4 3 ⇔ m = 0
Đáp án D
CM
26 tháng 7 2018
Đáp án A.
= x 2 − x 1 − 1 3 x 1 + x 2 2 − x 1 x 2 + m 2 x 1 + x 2 + 1
CM
25 tháng 7 2019
Có d qua điểm A(1;2) và có hệ số góc k có phương trình là d; y=k(x-1)+2
Phương trình hoành độ giao điểm: 
Khi đó diện tích hình phẳng
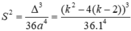
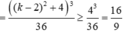
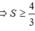
Chọn đáp án C.
*Chú ý diện tích hình phẳng giới hạn bởi parabol
y
=
a
x
2
+
b
x
+
c
và đường thẳng d:y=mx+n có công thức tính nhanh sau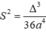 
trong đó Δ là biệt thức của phương trình hoành độ giao điểm:
CM
2 tháng 11 2017
Đáp án D
y ' = 4 a x 3 + 2 b x , y ' 1 = - 4 a - 2 b
Phương trình tiếp tuyến tại A là: d: y=(-4a-2b)(x+1)
Xét phương trình tương giao: a x 4 + b x 2 + c = ( - 4 a - 2 b ) ( x + 1 )
Phương trình có 2 nghiệm x=0,x=2 => 4 a + 2 b + c = 0 28 a + 10 b + c = 0 ( 1 )
∫ 0 2 - 4 a - 2 b x + 1 - a x 4 - b x 2 - c d x = - 2 a - b x 2 + - 4 a - 2 b x - a x 5 5 - b x 3 3 - c x 2 0 = - 112 5 a - 32 3 b - 2 c = 28 5 2 1 , 2 ⇒ a = 1 b = - 3 ⇒ y = x 4 - 3 x 2 + 2 , d : y = 2 x + 2 c = 2 ⇒ S = ∫ - 1 0 x 4 - 3 x 2 + 2 d x = x 5 5 - x 3 - x 2 0 - 1 = 1 5
CM
27 tháng 8 2017
Đáp án D
∫ 0 2 [ ( − 4 a − 2 b ) ( x + 1 ) − ax 4 − b x 2 − c ] d x = [ ( − 2 a − b ) x 2 + ( − 4 a − 2 b ) x − ax 5 5 − b x 3 3 − c x ] 2 0 = − 112 5 a − 32 3 b − 2 c = 28 5 ( 2 ) ( 1 ) , ( 2 ) ⇒ a = 1 b = − 3 c = 2 ⇒ y = x 4 − 3 x 2 + 2 , d : y = 2 x + 2 ⇒ S = ∫ − 1 0 ( x 4 − 3 x 2 + 2 ) d x = x 5 5 − x 3 − x 2 0 − 1 = 1 5
Đáp án D