Từ 9 học sinh gồm 4 học sinh giỏi, 3 học sinh khác, 2 học sinh trung bình, giáo viên muốn thành lập 3 nhóm làm 3 bài tập lớn khác nhau, mỗi nhóm 3 học sinh. Tính xác suất để nhóm nào cũng có học sinh giỏi và học sinh khá.
A. 3 70
B. 6 35
C. 9 35
D. 18 35



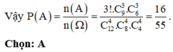
Chọn C.
Số phần tử của không gian mẫu là n ( Ω ) = C 9 3 . C 6 3 . C 3 3 .
Gọi X là biến cố “nhóm nào cũng có học sinh giỏi và học sinh khá”
Khi đó, ta xét các chia nhóm như sau:
· N1: 2 học sinh giỏi, 1 học sinh khá.
· N2: 1 học sinh giỏi, 1 học sinh khá và
· 1 học sinh trung bình.
· N3: 1 học sing giỏi, 1 học sinh khá
· và 1 học sinh trung bình.
Suy ra có 3 . ( C 4 2 . C 3 1 ) . C 2 1 . C 2 1 . C 2 1 cách chia ⇒ n ( X ) = 3 . C 4 2 . C 3 1 . C 2 1 . C 2 1 . C 2 1 .
Vậy xác suất cần tính là P = n ( X ) n ( Ω ) = 9 35