Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi A: “mỗi nhóm có đúng một học sinh nữ”.
+) Số cách xếp 3 học sinh nữ vào 3 nhóm là 3! cách.

+) Chọn 3 học sinh nam cho nhóm thứ ba có 1 cách.
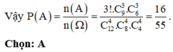

Đáp án A
Không gian mẫu: C 12 4 . C 8 4 . 1 = 34650
Chỉ có 3 nữ và chia mỗi nhóm có đúng 1 nữ và 3 nam.
Nhóm 2 có C 3 1 . C 9 3 = 252 cách.
Lúc đó còn lại 2 nữ, 6 nam, nhóm thứ 2 có :
C 2 1 . C 9 3 = 40 cách chọn.
Cuối cùng còn 4 người là một nhóm: có 1 cách.
Theo quy tắc nhân thì có: 252.40.2=10080 cách.
Vậy xác suất cần tìm là: P = 10080 34650 = 16 55 .

Đáp án B
Gọi x,y lần lượt là số học sinh nữ ở nhóm I và nhóm II. Khi đó số học sinh nam ở nhóm II là 25 − 9 + x − y = 16 − x − y . Điều kiện để mỗi nhóm đều có học sinh nam và nữ là x ≥ 1, y ≥ 1,16 − x − y ≥ 1 ; x , y ∈ ℕ .
Xác suất để chọn ra được hai học sinh nam bằng C 9 1 C 16 − x − y 1 C 9 + x 1 C 16 − x 1 = 0,54
⇔ 9 16 − x − y 9 + x 16 − x = 0,54 ⇔ 144 − 9 x − 9 y 144 + 7 x − x 2 = 0,54 ⇔ y = 184 25 − 71 50 x + 3 50 x 2
Ta có hệ điều kiện sau x ≥ 1 184 25 − 71 50 x + 3 50 x 2 ≥ 1 16 − x − 184 25 − 71 50 x + 3 50 x 2 ≥ 1 x ∈ ℕ
⇔ x ≥ 1 3 50 x 2 − 71 50 x + 159 25 ≥ 0 − 3 50 x 2 + 21 50 x + 191 25 ≥ 0 x ∈ ℕ ⇔ x ≥ 1 x ≥ 53 3 x ≤ 6 21 − 5 201 6 ≤ x ≤ 21 + 5 201 6 x ∈ ℕ ⇔ 1 ≤ x ≤ 6 x ∈ ℕ
Ta có bảng các giá trị của :
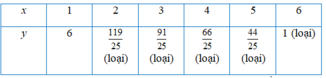
Vậy ta tìm được hai cặp nghiệm nguyên x ; y thỏa mãn điều kiện là 1 ; 6 và 6 ; 1 .
Xác suất để chọn ra hai học sinh nữ là C x 1 C y 1 C 9 + x 1 C 16 − x 1 = x y 9 + x 16 − x .
Nếu x ; y ∈ 1 ; 6 , 6 ; 1 thì xác suất này bằng 1 25 = 0,04 .

Chọn C.
Số phần tử của không gian mẫu là n ( Ω ) = C 9 3 . C 6 3 . C 3 3 .
Gọi X là biến cố “nhóm nào cũng có học sinh giỏi và học sinh khá”
Khi đó, ta xét các chia nhóm như sau:
· N1: 2 học sinh giỏi, 1 học sinh khá.
· N2: 1 học sinh giỏi, 1 học sinh khá và
· 1 học sinh trung bình.
· N3: 1 học sing giỏi, 1 học sinh khá
· và 1 học sinh trung bình.
Suy ra có 3 . ( C 4 2 . C 3 1 ) . C 2 1 . C 2 1 . C 2 1 cách chia ⇒ n ( X ) = 3 . C 4 2 . C 3 1 . C 2 1 . C 2 1 . C 2 1 .
Vậy xác suất cần tính là P = n ( X ) n ( Ω ) = 9 35

Đáp án B.
Không gian mẫu: Số cách chia 15 học sinh thành 5 nhóm, mỗi nhóm 3 học sinh:
n Ω = C 15 3 . C 12 3 . C 9 3 . C 6 3 . C 3 3 5 ! = 1401400.
Vì cả 5 nhóm đều có học sinh giỏi và khá nên sẽ có đúng 1 nhóm có 2 học sinh giỏi, 1 học
sinh khá, các nhóm còn lại đều có 1 giỏi, 1 khá và 1 trung bình.
Số kết quả thỏa mãn:
n P = C 6 2 . C 5 1 .4 ! .4 ! = 43200.
Xác suất cần tính:
n P n Ω = 216 7007 .

Đáp án D
Số cách chọn 3 học sinh trong nhóm làm 3 công việc là A 10 3 .

Đáp án D
Số cách chọn 3 em học sinh là số cách chọn 3 phần tử khác nhau trong 10 phần tử có phân biệt thứ tự nên số cách chọn thỏa yêu cầu là A 10 3


Đáp án D
Số cách chia tổ thành 3 nhóm đi làm 3 công việc khác nhau là C 12 4 . C 8 4 . C 4 4 = 34650
Với công việc thứ nhất có C 9 3 C 3 1 cách chọn 3 nam, 1 nữ.
Với công việc thứ nhất có C 6 3 C 2 1 cách chọn 3 nam, 1 nữ.
Với công việc thứ nhất có C 3 3 C 1 1 cách chọn 3 nam, 1 nữ.
Vậy xác suất cần tính là P = C 9 3 C 3 1 . C 6 3 C 2 1 . C 3 3 C 1 1 C 12 4 C 8 4 C 4 4 = 16 55