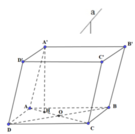
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng nhau (hình hộp như vậy còn được gọi là hình hộp thoi). Chứng minh rằng AC ⊥ B'D'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 1 2017
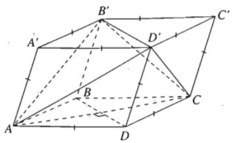
Theo giả thiết các mặt của hình hộp đều là hình thoi.
Ta có ABCD là hình thoi nên AC ⊥ BD
Theo tính chất của hình hộp: BD // B'D', do đó AC ⊥ B'D'.
Chứng minh tương tự ta được AB' ⊥ CD', AD' ⊥ CB'
Hai mặt phẳng (AA'C'C) và (BB'D'D) vuông góc với nhau khi hình hộp ABCD.A'B'C'D'là hình lập phương.
CM
19 tháng 10 2018
Trước hết dễ thấy tứ giác A'B'CD là hình bình hành, ngoài ra B′C = a = CD nên nó là hình thoi. Ta chứng minh hình thoi A'B'CD là hình vuông. Ta có:
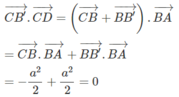
Vậy tứ giác A’B’CD là hình vuông.
CM
3 tháng 10 2017
Chọn A
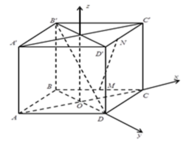
Đặt cạnh hình thoi ABCD là 1, chiều cao hình hộp = h (h>0).
Gọi O là giao điểm hai đường chéo AC và BD của hình thoi
Tam giác ABD đều
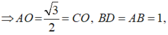
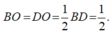
Ta có
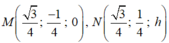
Lại có
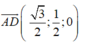
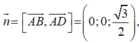
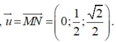
Gọi α là góc tạo bởi đường thẳng MN và mặt đáy (ABCD).
Ta có
CM
28 tháng 2 2018
Phương pháp:
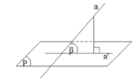
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Cách giải:
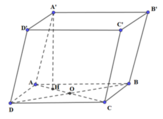
∆ AOD vuông tại O
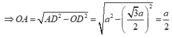
Thể tích khối hộp là: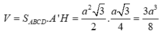 
Chọn: A
CM
4 tháng 1 2019
∆ A O D vuông tại O
⇒ O A = A D 2 - O D 2 = a 2 - 3 a 2 2 = a 2 ⇒ A H = 1 2 A O = a 4 ;
AC=2.AO=a và S A B C D = 1 2 . A C . B D
= 1 2 a . a . 3 = a 2 3 2
Do AA'//CC' nên
∠ ( A A ' ; ( A B C D ) ) = ∠ ( C C ' ; A B C D ) = 60 °
Do
A H ⊥ ( A B C D ) ⇒ ∠ ( A A ' ; ( A B C D ) ) = ∠ ( A A ' ; A H ) = ∠ A ' A H = 60 °
∆ A ' A H vuông tại
H ⇒ A ' H = A H . tan A ' A H = a 4 . tan 60 ° = a 3 4
Thể tích khối hộp là V = S A B C D . A ' H
= a 2 3 2 . a 3 4 = 3 a 3 8
Chọn đáp án A.
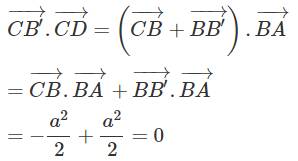
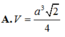
Từ giả thiết suy ra tứ giác ABCD là hình thoi, do đó AC ⊥ BD
Dễ thấy mặt chéo BDD'B' của hình hộp đã cho là hình bình hành, do đó BD // B′D′. Từ đó, theo bài 3.12 suy ra AC ⊥ B'D'.