Tìm số đo của góc giữa hai đường thẳng d1 và d2 lần lượt có phương trình: d1: 4x – 2y + 6 = 0 và d2: x – 3y + 1 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DL
1
9 tháng 5 2021
- Xét d1 và d2 có : \(\left\{{}\begin{matrix}\overrightarrow{n_{d1}}\left(1;-3\right)\\\overrightarrow{n_{d2}}\left(1;-2\right)\end{matrix}\right.\)
\(\Rightarrow\cos\alpha=\left|\dfrac{\overrightarrow{n_{d1}}.\overrightarrow{n_{d2}}}{\left|\overrightarrow{n_{d1}}\right|.\left|\overrightarrow{n_{d2}}\right|}\right|=\left|\dfrac{1.1+\left(-2\right).\left(-3\right)}{\sqrt{\left(1^2+\left(-3\right)^2\right)\left(1^2+\left(-2\right)^2\right)}}\right|=\dfrac{7\sqrt{2}}{10}\)
\(\Rightarrow\alpha=~8^o\)
- Từ d1 và d2 ta có hệ phương trình \(\left\{{}\begin{matrix}x-3y=-1\\x-2y=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=17\\y=6\end{matrix}\right.\)
Vậy tọa độ giao điểm của d1 và d2 là ( 17; 6 ) .
CM
20 tháng 12 2019
Đáp án D
Gọi I là giao điểm của hai đường thẳng d1; d2 . Tọa độ điểm I là nghiệm của hệ:
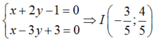
Lấy điểm m 1 ; 0 ∈ d 1 . Đường thẳng qua M và vuông góc với d2 có phương trình: 3x + y-3= 0
Gọi H = ∆ ∩ d 2 suy ra tọa độ điểm H là nghiệm của hệ:
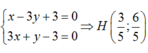
Phương trình đường thẳng
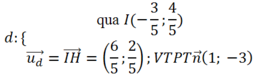
có dạng:
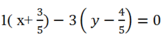
hay x-3y + 3= 0
CM
23 tháng 2 2017
Đáp án: A
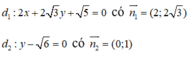
Gọi α là góc giữa hai đường thẳng d1, d2
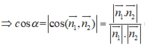
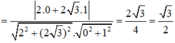
⇒ α = 30 °
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2022
\(d_1\) nhận \(\overrightarrow{n_1}=\left(1;2\right)\) là 1 vtpt
\(d_2\) nhận \(\overrightarrow{n_2}=\left(2;-1\right)\) là 1 vtpt
Do \(\overrightarrow{n_1}.\overrightarrow{n_2}=1.2+2.\left(-1\right)=0\Rightarrow d_1\perp d_2\)
hay góc giữa 2 đường thẳng là 90 độ
CM
2 tháng 9 2018
Đáp án D
+Giao điểm của d1 và d2 là nghiệm của hệ
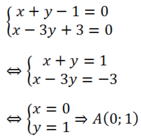
+Lấy M(1 ; 0) thuộc d1. Tìm M’ đối xứng M qua d2
+Viết phương trình đường thẳng ∆ đi qua M và vuông góc với d2 là
3(x-1) + 1( y=0) =0 hay 3x+ y-3= 0
Gọi H là giao điểm của ∆ và đường thẳng d2. Tọa độ H là nghiệm của hệ
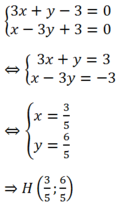
Ta có H là trung điểm của MM’. Từ đó suy ra tọa độ:
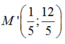
Viết phương trình đường thẳng d đi qua 2 điểm A và M’ : đi qua A(0 ;1) , vectơ chỉ phương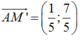 
=> vectơ pháp tuyến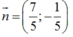 
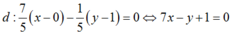
L
12 tháng 7 2015
A = AB giao d1=> Tọa độ A là nghiệm của hệ : \(\begin{cases}5x-3y+2=0\\4x-3y+1=0\end{cases}\)<=> \(\begin{cases}x+1=0\\4x-3y+1=0\end{cases}\)<=> \(\begin{cases}x=-1\\y=\frac{1+4x}{3}\end{cases}\)<=> \(\begin{cases}x=-1\\y=-1\end{cases}\)=> A (-1; -1)
Đường thẳng d2 có vtpt là \(\vec{n_2}\left(7;2\right)\) chính là vtcp của đường thẳng AC , điểm A thuộc AC
=> Phương trình đường thẳng AC có dạng: \(\begin{cases}x=-1+7t\\y=-1+2t\end{cases}\)(t \(\in\) R)
Gọi H = d1 \(\cap\) d2 => tọa độ H là nghiệm của pt: \(\begin{cases}7x+2y-22=0\\4x-3y+1=0\end{cases}\) <=> \(\begin{cases}x=\frac{64}{29}\\y=\frac{95}{29}\end{cases}\)=> H (\(\frac{64}{29};\frac{95}{29}\))
Đường cao CH đi qua H và có vtcp chính là vtpt của AB là \(\vec{n}\) (5; -3)
=> Phương trình CH có dạng : \(\begin{cases}x=\frac{64}{29}+5t\\y=\frac{95}{29}-3t\end{cases}\)
B = AB \(\cap\) d2 => Tọa độ B là nghiệm của hệ : \(\begin{cases}5x-3y+2=0\\7x+2y-22=0\end{cases}\) <=> \(\begin{cases}x=2\\y=4\end{cases}\)=> B (2;4)
Đường thẳng BC đi qua B , có vtcp chính là vtpt của d1 là \(\vec{n_1}\)(4;-3)
=> phương trình đường thẳng BC là: \(\begin{cases}x=2+4t\\y=4-3t\end{cases}\)
TC
1
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 4 2022
Gọi M là giao điểm \(d_1;d_2\Rightarrow\) tọa độ M thỏa mãn:
\(\left\{{}\begin{matrix}x+2y-1=0\\x-3y+3=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{3}{5}\\y=\dfrac{4}{5}\end{matrix}\right.\) \(\Rightarrow M\left(-\dfrac{3}{5};\dfrac{4}{5}\right)\)
Chọn \(N\left(1;0\right)\) là 1 điểm thuộc \(d_1\)
Gọi \(d_3\) là đường thẳng qua N và vuông góc \(d_2\Rightarrow d_3\) nhận (3;1) là 1 vtpt
Phương trình \(d_3\):
\(3\left(x-1\right)+1\left(y-0\right)=0\Leftrightarrow3x+y-3=0\)
Gọi P là giao điểm \(d_2;d_3\Rightarrow\) tọa độ P là nghiệm:
\(\left\{{}\begin{matrix}3x+y-3=0\\x-3y+3=0\\\end{matrix}\right.\) \(\Rightarrow P\left(\dfrac{3}{5};\dfrac{6}{5}\right)\)
Gọi Q là điểm đối xứng N qua \(d_2\Rightarrow P\) là trung điểm NQ
\(\Rightarrow\left\{{}\begin{matrix}x_Q=2x_P-x_N=\dfrac{1}{5}\\y_Q=2y_P-y_N=\dfrac{12}{5}\end{matrix}\right.\) \(\Rightarrow Q\left(\dfrac{1}{5};\dfrac{12}{5}\right)\)
\(\Rightarrow MQ\) đối xứng \(MN\) qua \(d_2\Rightarrow MQ\) là đường thẳng d cần tìm
\(\overrightarrow{MQ}=\left(\dfrac{4}{5};\dfrac{8}{5}\right)=\dfrac{4}{5}\left(1;2\right)\) \(\Rightarrow\) đường thẳng d nhận (2;-1) là 1 vtpt
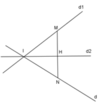
Phương trình d:
\(2\left(x-\dfrac{1}{5}\right)-1\left(y-\dfrac{12}{5}\right)=0\Leftrightarrow2x-y+2=0\)
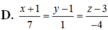
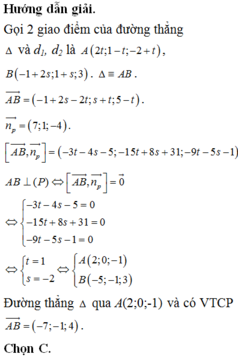
Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :