Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(d_1\) nhận \(\overrightarrow{n_1}=\left(1;2\right)\) là 1 vtpt
\(d_2\) nhận \(\overrightarrow{n_2}=\left(2;-1\right)\) là 1 vtpt
Do \(\overrightarrow{n_1}.\overrightarrow{n_2}=1.2+2.\left(-1\right)=0\Rightarrow d_1\perp d_2\)
hay góc giữa 2 đường thẳng là 90 độ

Đáp án: A
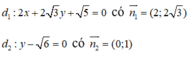
Gọi α là góc giữa hai đường thẳng d1, d2
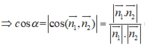
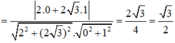
⇒ α = 30 °

Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :
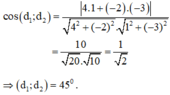

\(\left\{{}\begin{matrix}x=4+2t\\y=1-5t\end{matrix}\right.\)
Vậy: VTCP là (2;-5) và điểm mà (d1) đi qua là A(4;1)
=>VTPT là (5;2)
Phương trình đường thẳng của (d1) là:
5(x-4)+2(y-1)=0
=>5x-20+2y-2=0
=>5x+2y-22=0
(d2): 2x-5y-14=0
=>(d1) và (d2) vuông góc

ĐÁP ÁN B
Đường thẳng qua A và tạo với d1d2 các góc bằng nhau khi vuông góc với phân giác của góc tạo bởi d1d2.
Do vậy số lượng đường thẳng cần tìm là 2.

Vectơ pháp tuyến của đường thẳng d1 là n1=(1;2)
Vectơ pháp tuyến của đường thẳng d2 là n2=(2;-4)
Gọi φ là góc giữa 2 đường thẳng ta có:
cos φ = n 1 . n 2 n 1 . n 2 = - 3 5
Chọn A.

Lời giải:
Vì $A\in (d_1)$ nên gọi tọa độ của $A$ là $(a, 2a-2)$
Vì $B\in (d_2)$ nên gọi tọa độ của $B$ là $(b, -b-3)$
$M$ là trung điểm của $AB$ nên:
\(3=x_M=\frac{x_A+x_B}{2}=\frac{a+b}{2}\Rightarrow a+b=6(1)\)
\(0=y_M=\frac{y_A+y_B}{2}=\frac{2a-2-b-3}{2}\Rightarrow 2a-b=5(2)\)
Từ $(1); (2)\Rightarrow a=\frac{11}{3}; b=\frac{7}{3}$
Khi đó: $A=(\frac{11}{3}, \frac{16}{3})$
Vì $A, M\in (d)$ nên VTCP của (d) là $\overrightarrow{MA}=(\frac{2}{3}, \frac{16}{3})$
$\Rightarrow \overrightarrow{n_d}=(\frac{-16}{3}, \frac{2}{3})$
PTĐT $(d)$ là:
$\frac{-16}{3}(x-3)+\frac{2}{3}(y-0)=0$
$\Leftrightarrow -8x+y+24=0$

- Xét d1 và d2 có : \(\left\{{}\begin{matrix}\overrightarrow{n_{d1}}\left(1;-3\right)\\\overrightarrow{n_{d2}}\left(1;-2\right)\end{matrix}\right.\)
\(\Rightarrow\cos\alpha=\left|\dfrac{\overrightarrow{n_{d1}}.\overrightarrow{n_{d2}}}{\left|\overrightarrow{n_{d1}}\right|.\left|\overrightarrow{n_{d2}}\right|}\right|=\left|\dfrac{1.1+\left(-2\right).\left(-3\right)}{\sqrt{\left(1^2+\left(-3\right)^2\right)\left(1^2+\left(-2\right)^2\right)}}\right|=\dfrac{7\sqrt{2}}{10}\)
\(\Rightarrow\alpha=~8^o\)
- Từ d1 và d2 ta có hệ phương trình \(\left\{{}\begin{matrix}x-3y=-1\\x-2y=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=17\\y=6\end{matrix}\right.\)
Vậy tọa độ giao điểm của d1 và d2 là ( 17; 6 ) .
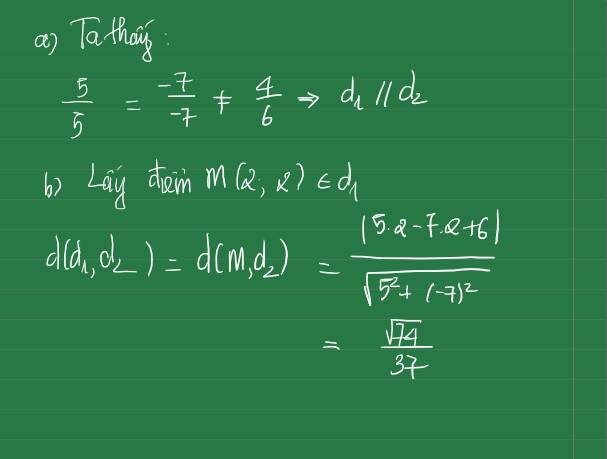
Chọn A
A