Cho dãy số ( u n ) với u n = ( - 1 ) n - 1 n + 1 . Khẳng định nào sau đây sai?
A. Số hạng thứ 9 của dãy số là 1 10
B. Dãy số ( u n ) bị chặn
C. Dãy số ( u n ) là một dãy số giảm
D. Số hạng thứ 10 của dãy số là - 1 11
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Phương pháp: Tìm công thức số hạng tổng quát
Cách giải: Ta có:
u ( 1 ) = 1
u ( 2 ) = u ( 1 ) + u ( 1 ) = 2 u ( 1 ) + 1
u ( 3 ) = u ( 2 ) + u ( 1 ) = 3 u ( 1 ) + 1 + 2
u ( 4 ) = u ( 3 ) + u ( 1 ) = 4 u ( 1 ) + 1 + 2 + 3
. . .
u ( 2017 ) = u ( 2016 ) + u ( 1 ) = 2017 u ( 1 ) + 1 + 2 + 3 . . . + 2016
⇒ u ( 2017 ) = 1 + 2 + 3 . . . + 2016 + 2017 = 2035153

Xét `H=u_[n+1]-u_n`
`=1/[n+3]-1/[n+2]`
`=[n+2-n-3]/[(n+3)(n+2)]=[-1]/[(n+3)(n+2)]`
Với `n in NN`*`=>(n+3)(n+2) > 0<=>[-1]/(n+3)(n+2)] > 0`
`=>H > 0`
`->\bb D`
Chọn B, do mọi số hạng của dãy số này đều lớn hơn 0.

Chọn A.
Ta có: 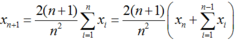
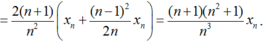
Do đó: 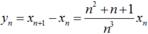
- Ta chứng minh dãy (yn) tăng.
Ta có: 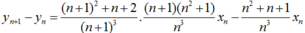
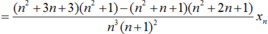
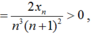
- Ta chứng minh dãy (yn) bị chặn.
Trước hết ta chứng minh: xn ≤ 4(n – 1) (1)
* Với n = 2, ta có: x2 = 4x1 = 4 nên (1) đúng với n = 2
* Giả sử (1) đúng với n, tức là: xn ≤ 4(n – 1), ta có
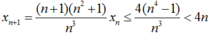
Nên (1) đúng với n + 1. Theo nguyên lí quy nạp ta suy ra (1) đúng
Ta có: 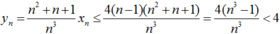
Vậy bài toán được chứng minh.

1. a) Lấy biến C để tính un và E để tính sn và D là biến đếm. Ta có quy trình bấm phím liên tục
D=D+1:C=2B+A:E=E+C:A=B:B=C
CALC giá trị A=2; B=20; D=2; E=22 nhấn "=" liên tục
Kết quả: u20 = 137990600; s20 = 235564680; u30 = 928124755084; s30 = 1584408063182
2. Lấy A làm biến lẻ, B làm biến chẵn, C là tổng S, D là biến đếm. Ta có quy trình bấm phím liên tục
D=D+1:A=2B+3A:C=C+A:D=D+1:B=2A+3B:C=C+B
CALC giá trị D=2; A=1; B=2; C=3 nhấn "=" liên tục
a) Kết quả: u10 = 28595; u15 = 8725987; u20 = 3520076983
b) Kết quả: s10 = 40149; s15 =13088980 ; s20 = 4942439711
Chọn C
Dễ thấy u n = ( - 1 ) n - 1 n + 1 = 1 n + 1 < 1 , ∀ n ∈ ℕ *
nên ( u n ) là dãy số bị chặn
Lại có u 9 = 1 10 ; u 10 = - 1 11 ; u 11 = 1 12 ; u 12 = - 1 13
Suy ra dãy ( u n ) không phải là dãy số tăng cũng không phải là dãy số giảm.
Do đó đáp án C sai