Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
u n + 1 − u n = − n + 1 2 + n + 1 + 1 − − n 2 + n + 1 = − n 2 − 2 n − 1 + n + 2 + n 2 − n − 1 = − 2 n < 0 ∀ n ≥ 1
Do đó ( u n ) là một dãy giảm.
Chọn đáp án D

Chọn C
Dễ thấy u n = ( - 1 ) n - 1 n + 1 = 1 n + 1 < 1 , ∀ n ∈ ℕ *
nên ( u n ) là dãy số bị chặn
Lại có u 9 = 1 10 ; u 10 = - 1 11 ; u 11 = 1 12 ; u 12 = - 1 13
Suy ra dãy ( u n ) không phải là dãy số tăng cũng không phải là dãy số giảm.
Do đó đáp án C sai

Chọn A.
Ta có un+12 = 2010 + un ⇒ un+1 – un = -un+12 + un+1 + 2010
Bằng quy nạp ta chứng minh được 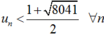
Suy ra un+1 – un > 0 ⇒ dãy (un) là dãy tăng.

Đáp án D
Xét u 2018 v 2018 = S 2018 - S 2017 T 2018 - T 2017 = 3 5

Hướng dẫn giải.
Phương pháp loại trừ: C hoặc D sai.
Thật vậy
u n + 1 = 2 ( n + 1 ) + 5 = u n + 2 ∀ n ∈ ℕ *
⇒ đáp án C sai.
Chọn C

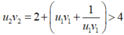
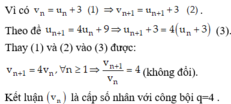
Xét `H=u_[n+1]-u_n`
`=1/[n+3]-1/[n+2]`
`=[n+2-n-3]/[(n+3)(n+2)]=[-1]/[(n+3)(n+2)]`
Với `n in NN`*`=>(n+3)(n+2) > 0<=>[-1]/(n+3)(n+2)] > 0`
`=>H > 0`
`->\bb D`
Chọn B, do mọi số hạng của dãy số này đều lớn hơn 0.