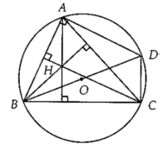
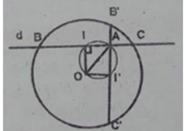
Cho hai điểm B,C cố định trên đường tròn (O,R) và A thay đổi trên đường tròn đó, BD là đường kính. Khi đó quỹ tích trực tâm H của ∆ A B C là.
A. Đoạn thẳng nối từ A tới chân đường cao thuộc BC của ∆ A B C .
B. Cung tròn của đường tròn đường kính BC.
C. Đường tròn tâm O' bán kính R là ảnh của (O,R) qua T H A ¯ .
D. Đường tròn tâm O' bán kính R là ảnh của (O/R) qua T D C ¯ .