Cho đồ thị hàm số y=f(x) có lim x → + ∞ f x = 0 và lim x → - ∞ f x = + ∞ . Mệnh đề nào sau đây là mệnh đề đúng?
A. Đồ thị hàm số không có tiệm cận ngang
B. Đồ thị hàm số nằm phía trên trục hoành
C. Đồ thị hàm số có một tiệm cận đứng là đường thẳng y=0
D. Đồ thị hàm số có một tiệm cận ngang là trục hoành


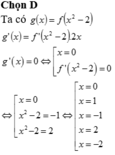

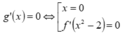
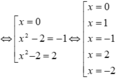
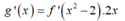
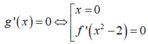
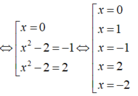

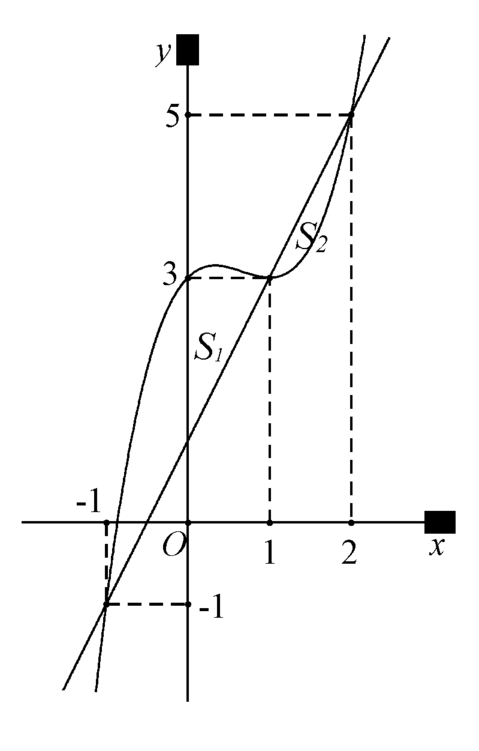
 là
là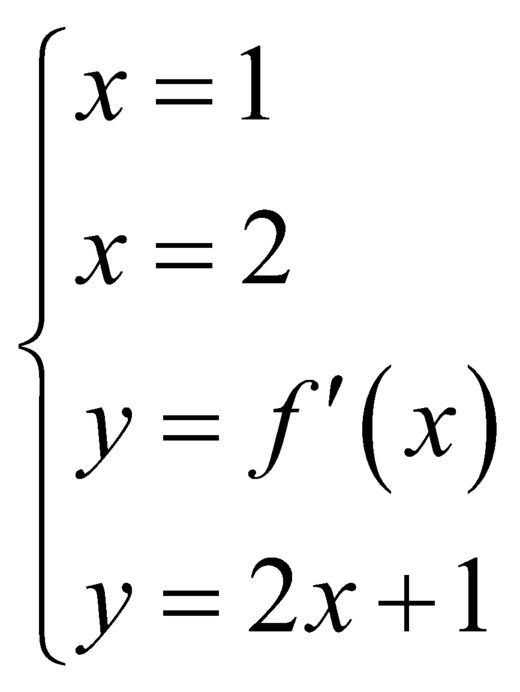 là
là
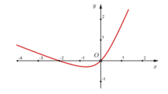

Chọn đáp án D
Phương pháp
+) Đường thẳng x=a được gọi là TCĐ của đồ thị hàm số
+) Đường thẳng y=b được gọi là TCN của đồ thị hàm số