Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Xét hàm số ![]() . Khi đó hàm số
. Khi đó hàm số ![]() liên tục trên các đoạn
liên tục trên các đoạn ![]() ,
, ![]() và có
và có ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() .
.
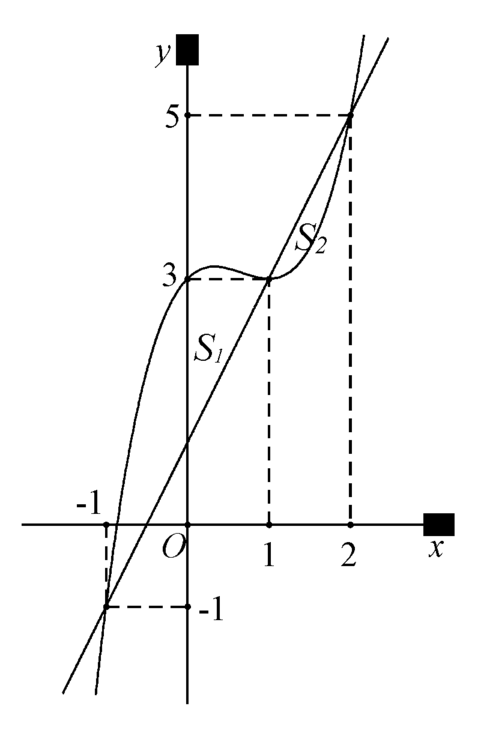
Do đó diện tích hình phẳng giới hạn bởi 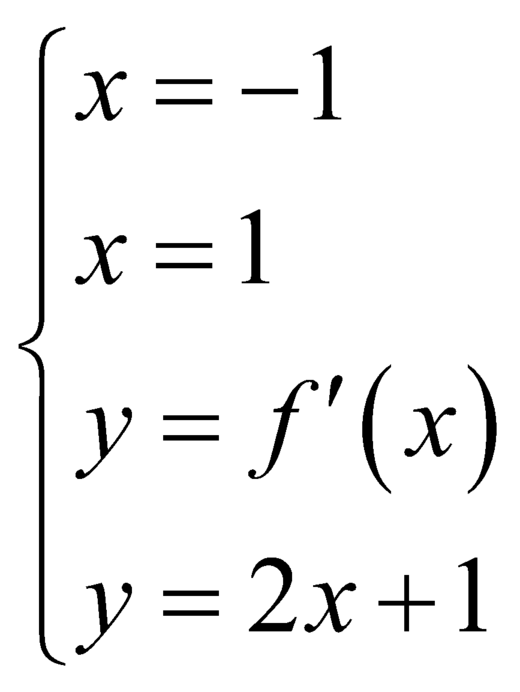 là
là
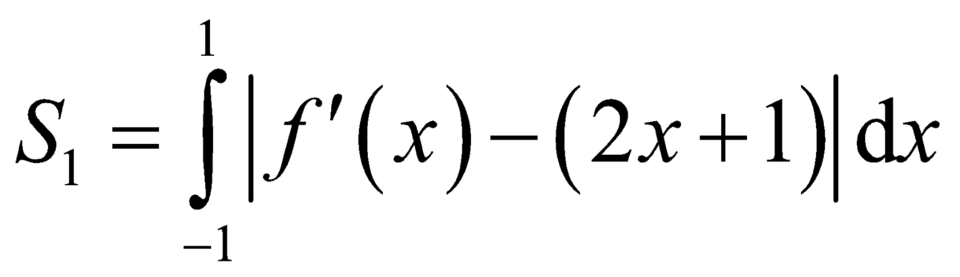
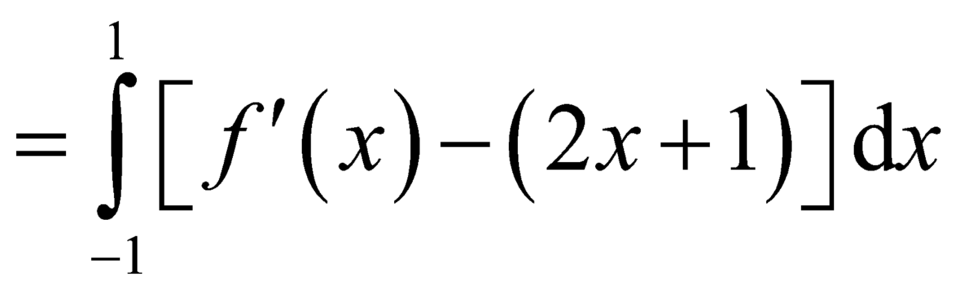
![]()
![]() .
.
Vì ![]() nên
nên ![]() .
.
Diện tích hình phẳng giới hạn bởi 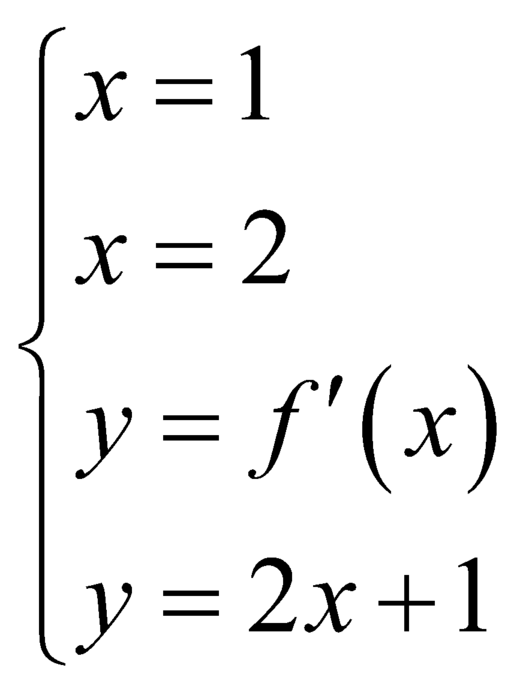 là
là
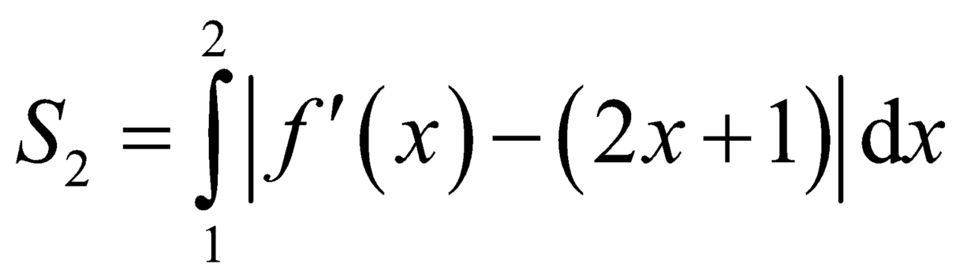
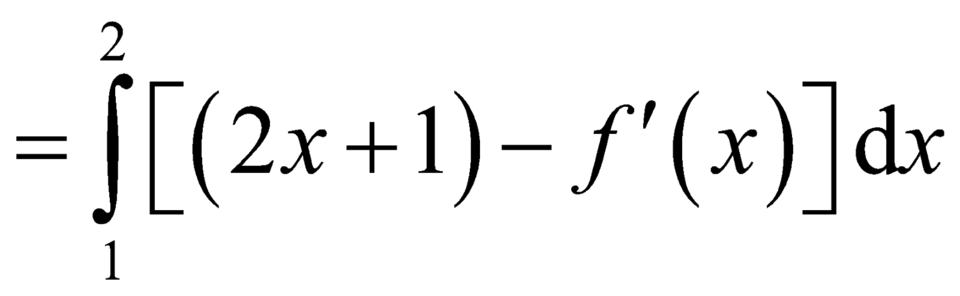
![]()
![]() .
.
Vì ![]() nên
nên ![]() .
.

Chọn C
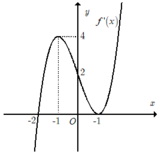
+ ta có: f’( x) = 0 khi x= -1 hoặc x= -2.
+ Giá trị của hàm số y= f’(x) không đổi dấu khi đi qua x= - 1 nên x= -1 không là điểm cực trị của hàm số.
+ Giá trị của hàm số y= f’(x) đổi dấu từ âm sang dương khi qua x= -2
=> Hàm số y= f(x) đạt cực tiểu tại điểm x= -2.

Ta có:
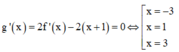
Với x< - 3 ta có: f’ (x)< x= 1 suy ra hàm số nghịch biến trên khoảng ( -∞; -3)
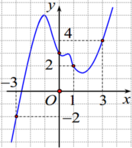
+ xét hàm số g( x) ; ta cần so sánh g( -3) và g( 3)
Ta có g(x) = 2f(x) –( x+ 1) 2 nên g’ (x) =2f’ (x) -2(x+1)
Phương trình 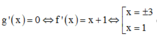 (Dựa vào đồ thị hàm số y= f’ (x)) .
(Dựa vào đồ thị hàm số y= f’ (x)) .
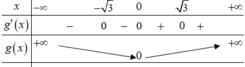
Bảng xét dấu của g’(x)

Dựa vào bảng xét dấu, ta được m a x [ - 3 ; 3 ] g ( x ) = g ( 1 ) .
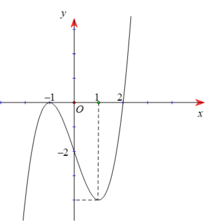
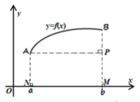
Dựa vào hình vẽ lại có
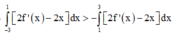
Do đó g( 1) – g( -3) > g( 1) – g( 3) hay g( 3) > g( -3) .
Suy ra GTNN của hàm số trên đoạn [- 3; 3] là g( -3) .
Chọn B.
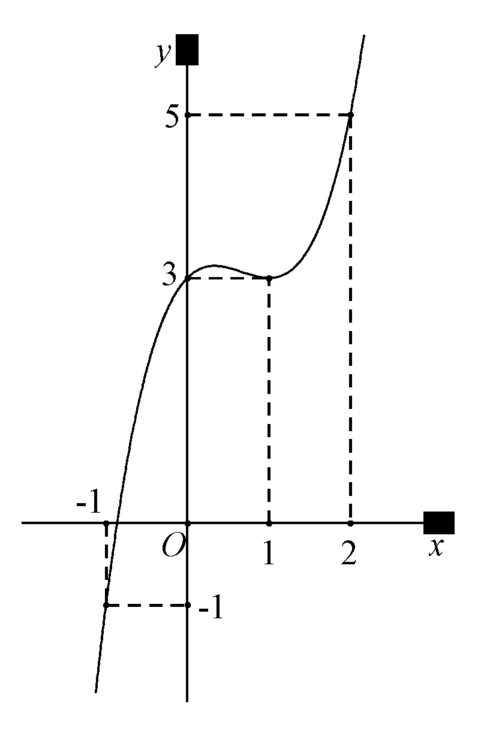



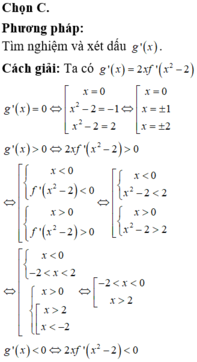



Chọn D
Xét hàm số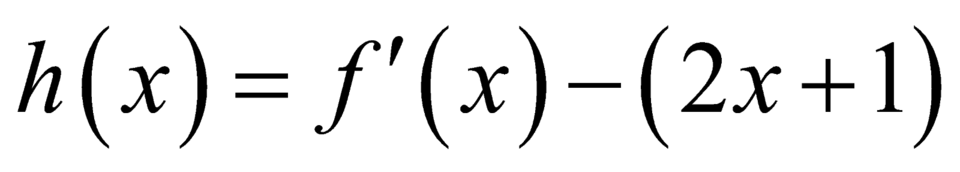 . Khi đó hàm số
. Khi đó hàm số 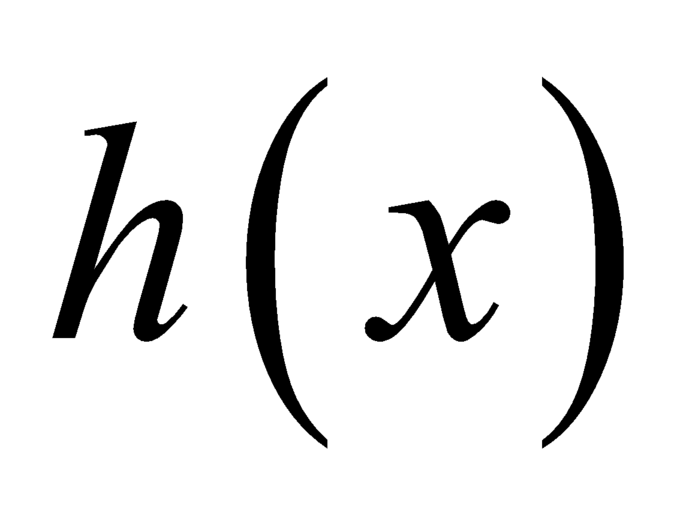 liên tục trên các đoạn
liên tục trên các đoạn 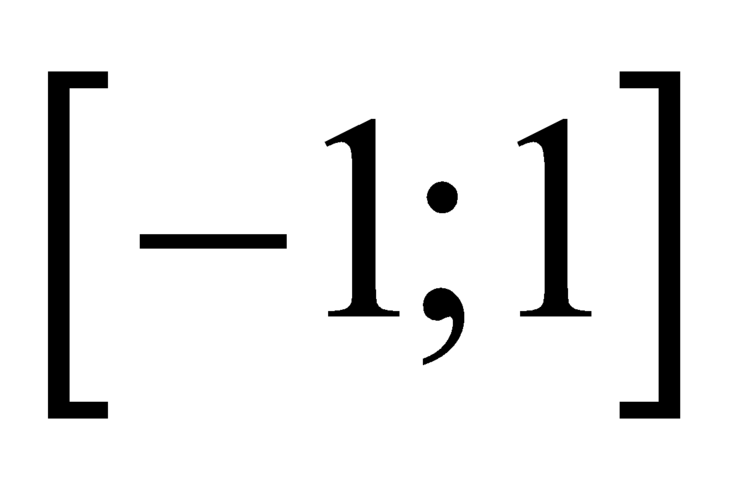 ,
, 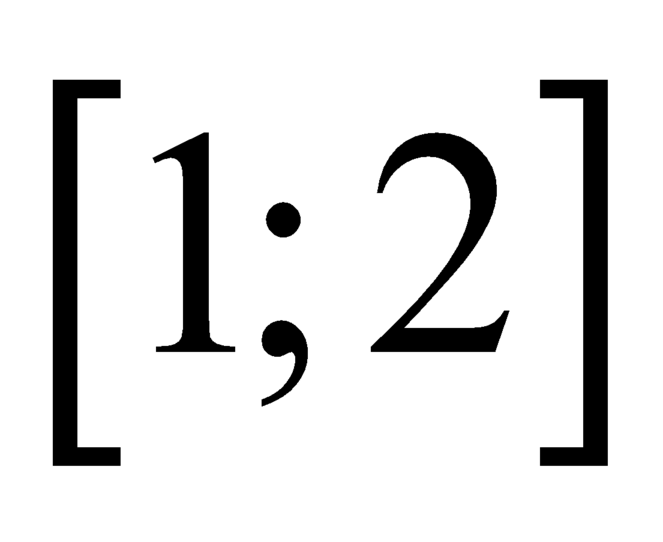 và có
và có 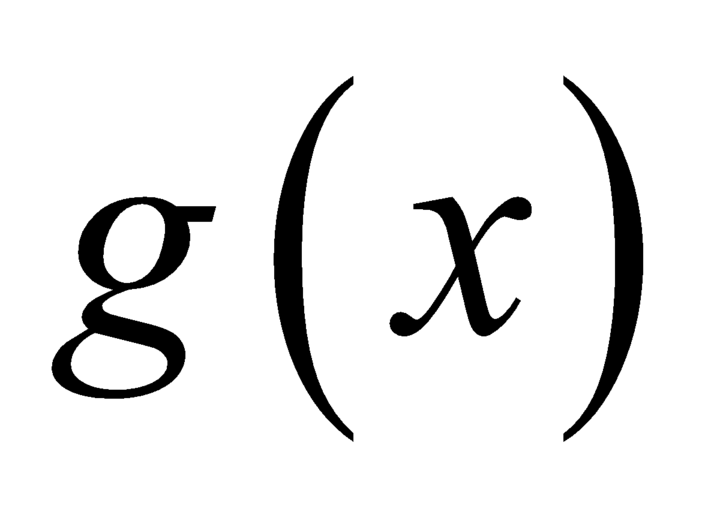 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 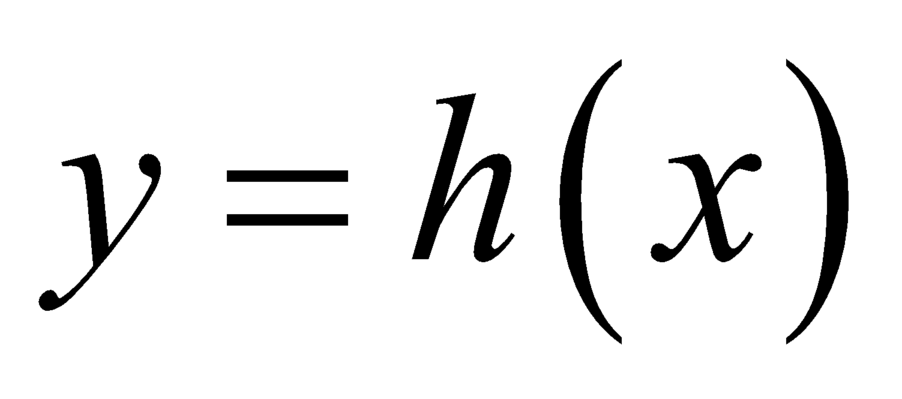 .
.
Do đó diện tích hình phẳng giới hạn bởi là
là
Vì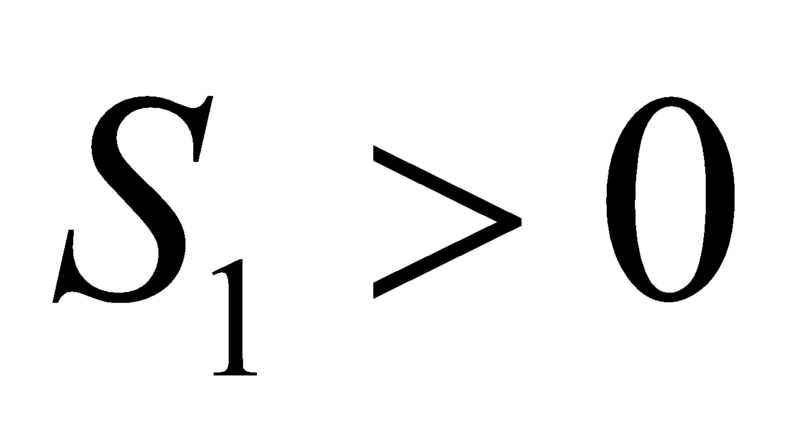 nên
nên 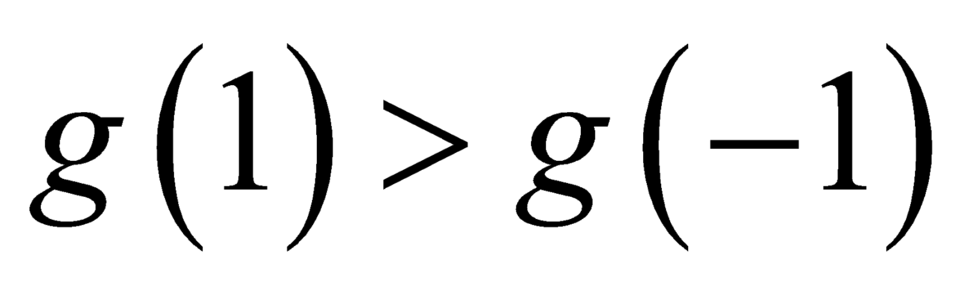 .
.
Diện tích hình phẳng giới hạn bởi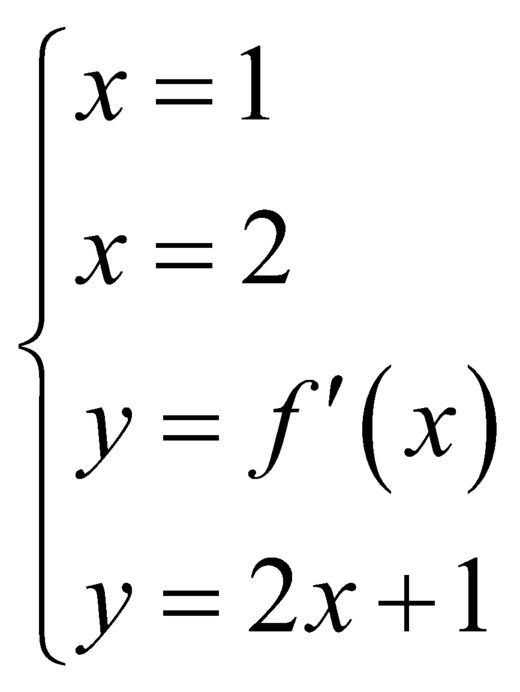 là
là
Vì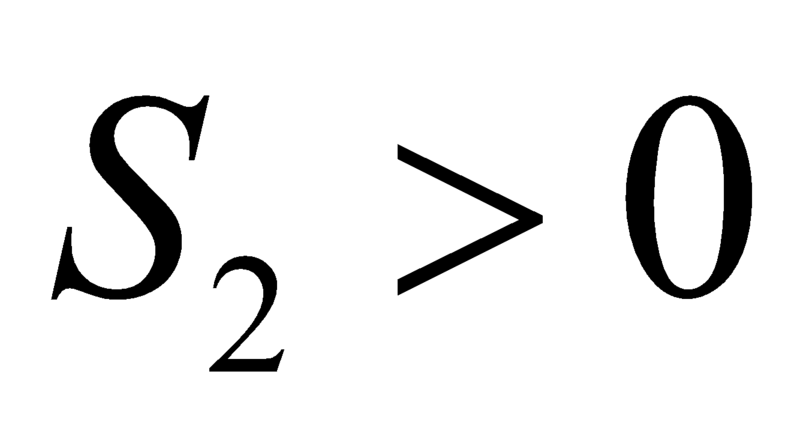 nên
nên 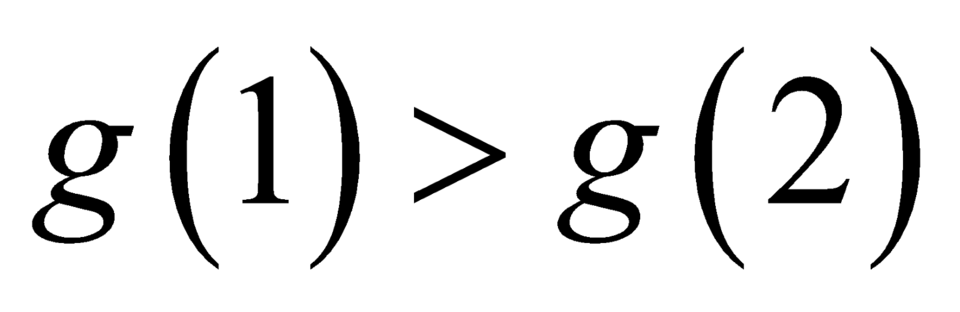 .
.