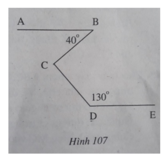
Cho hình 107 trong đó ∠B = 40o, ∠D = 130o, AB // DE. Tính ∠BCD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 7 2021
(a+b) theo mình thì DAC=140o
*Kéo dài BA để BA cắt CF tại K
Kéo dài CA để CA cắt BE tại H
*ta có: K= A-C=90 độ-40 độ= 50 độ
B cũng = 50 độ
mà 2 góc này nằm ở vị trí so le trong => EB // CF(1)
* ta có: H=A-B=90 độ - 50 độ= 40 độ
=> EHA= 180 độ- 40 độ = 140 độ. DAC cũng =140 độ
mà 2 góc này đồng vị
=> DA//EB(2)
từ 1,2=> a) và b) đúng
KD
26 tháng 7 2021
Kẻ Cz // AB
⇒ˆABC+ˆBCz=180°⇒ABC^+BCz^=180°(2 góc trrong cùng phía bù nhau)
Ta có: ˆABC+ˆBCD+ˆCDE=360°ABC^+BCD^+CDE^=360°
=ˆABC+ˆBCz+ˆzCD+ˆCDE=360°=ABC^+BCz^+zCD^+CDE^=360°
⇒180°+ˆzCD+ˆCDE=360°⇒180°+zCD^+CDE^=360°
⇒ˆzCD+ˆCDE=360°−180°=180°⇒zCD^+CDE^=360°-180°=180° mà 2 góc này nằm ở vị trí trong cùng phía
=> DE // Cz mà Cz // AB
=> AB // DE (đpcm)
4 tháng 2 2022
a: Xét (O) có
OH là một phần đường kính
CD là dây
OH\(\perp\)CD tại H
Do đó: H là trung điểm của CD
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
b: Xét tứ giác ACED có
H là trung điểm của AE
H là trung điểm của CD
Do đó: ACED là hình bình hành
mà AE\(\perp\)CD
nên ACED là hình thoi
Suy ra: DE//AC
mà AC\(\perp\)CB
nên DE\(\perp\)BC
19 tháng 5 2022
a: \(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
b: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
Do đó;ΔABC=ΔADC
Suy ra: CB=CD
hay ΔCBD cân tại C
c: Xét ΔCBD có
CA là đường trung tuyến
CE=2/3CA
Do đó: E là trọng tâm của ΔCBD
=>DE đi qua trung điểm của BC
15 tháng 3 2022
a: AC=4cm
b: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD
DO đó: ΔCAB=ΔCAD
SUy ra: CB=CD
hay ΔCBD cân tại C
c: Xét ΔCDB có
CA là đường trung tuyến
CE=2/3CA
Do đó: E là trọng tâm
=>DE đi qua trung điểm của BC
Kẻ CK // AB. Do CK // AB, DE // AB nên CK // DE.
AB // CK ⇒ ∠BCK = ∠B = 40° (so le trong)
CK // DE ⇒ ∠DCK + ∠CDE = 180° ( hai góc trong cùng phía bù nhau )
⇒ ∠DCK = 180° - ∠CDE = 180° - 130° = 50°.
Do đó: ∠BCD = ∠BCK + ∠DCK = 40° + 50° = 90°.