KT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 9 2018
Hình nào?
không có hình thì làm làm sao được?
Bạn vẽ hình đi :)
NQ
0
13 tháng 3 2022
a) Xét \(\Delta ABD\) và \(\Delta AED\) có :
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
=> \(\Delta ABD\) =\(\Delta AED\) (c-g-c)
=> DE=DB ; \(\widehat{ABD}=\widehat{AED}\)
b)Có : \(\widehat{ABD}+\widehat{MBD}=180^o\)
\(\widehat{AED}+\widehat{DEC}=180^o\)
mà \(\widehat{ABD}=\widehat{AED}\) => \(\widehat{MBD}=\widehat{DEC}\)
Xét \(\Delta MDBvà\Delta CDE\) có :
\(\widehat{MBD}=\widehat{DEC}\)
DE=DB
\(\widehat{MBD}=\widehat{CDE}\)
=> \(\Delta MDB=\Delta CDE\left(g-c-g\right)\)
c) Có : AB=AE ( \(\Delta ABD\) =\(\Delta AED\) )
MB=CE(\(\Delta MDB=\Delta CDE\))
=> AB+BM=AE+EC
=> AM=AC
=> \(\Delta MAC\) cân tại A
mà AD là tia phân giác của góc A
=> AD là đường cao của \(\Delta MAC\)
=> \(AD\perp MC\)
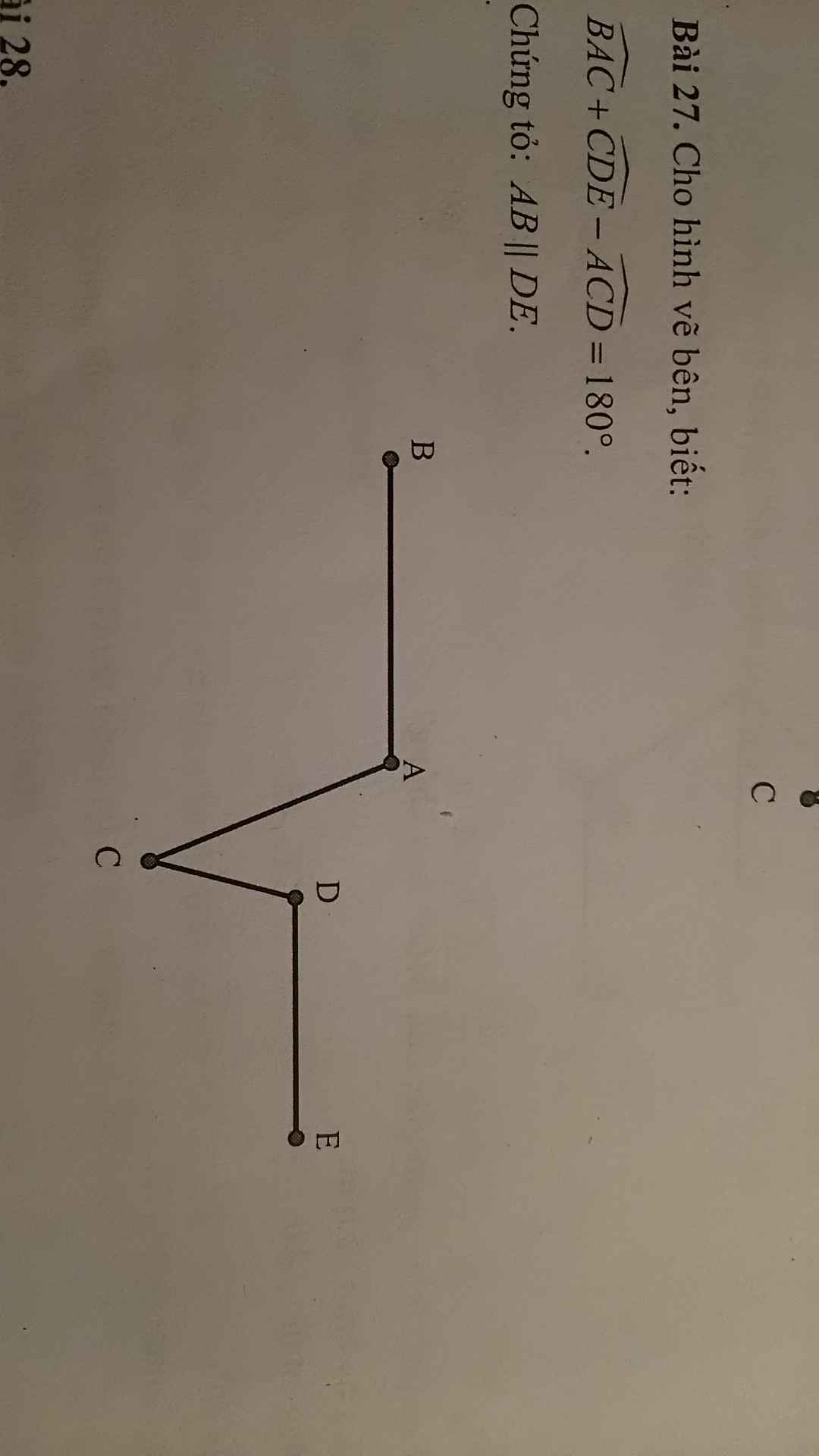
Giải thích các bước giải:Kẻ Cz // AB
⇒ˆABC+ˆBCz=180°⇒ABC^+BCz^=180°(2 góc trrong cùng phía bù nhau)
Ta có: ˆABC+ˆBCD+ˆCDE=360°ABC^+BCD^+CDE^=360°
=ˆABC+ˆBCz+ˆzCD+ˆCDE=360°=ABC^+BCz^+zCD^+CDE^=360°
⇒180°+ˆzCD+ˆCDE=360°⇒180°+zCD^+CDE^=360°
⇒ˆzCD+ˆCDE=360°−180°=180°⇒zCD^+CDE^=360°-180°=180° mà 2 góc này nằm ở vị trí trong cùng phía
=> DE // Cz mà Cz // AB
=> AB // DE (đpcm)