Tìm các giá trị của m để hai bất phương trình x < − 2 và x < m 2 + 4 m − 9 2 tương đương.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 11 2018
Chọn D.
+) (m + 2)x ≤ m + 1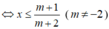 
+) 3m(x - 1) ≤ -x - 1 ⇔ 3mx - 3m + x + 1 ≤ (3m + 1)x ≤ 3m - 1
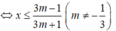
Hai bất phương trình (m + 2)x ≤ m + 1 và 3m(x - 1) ≤ -x - 1 tương đương khi và chỉ khi hai bất phương trình có cùng tập nghiệm khi đó:
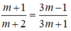
⇔ (m + 1)(3m + 1) = (m + 2)(3m - 1)
⇔ 3 m 2 + m + 3m + 1 = 3 m 2 - m + 6m - 2
⇔ 3 m 2 + m + 3m + 1 - 3 m 2 + m - 6m + 2 = 0
⇔ -m + 3 = 0
⇔ m = 3 (thỏa mãn)
18 tháng 4 2020
Giải pt (1) :(x+3)(2x+1)=0
=>{x+3=0 / {2x+1=0
=> {x=-3 / {x=-1/2
Để hai pt tương đương thì pt (2) nhận giá trị x=-3 và x=-1/2 .
+)Thay x=-3 vào pt (2) :
(m-4)(-3)^2 - 2(2m+9)(-3) -4 =0
=> (m-4)9 + 6(2m+9) - 4 = 0
=> 9m - 36+ 12m + 54 - 4= 0
=> 21m + 14 = 0
=> 21m = -14
=> m= -2/3
Vậy ...
18 tháng 4 2020
+) Thay x= -1/2 vào pt (2) :
(m-4)(-1/2)^2 - 2(2m+9)(-1/2) -4 =0
=>1/4(m-4) + 2m +9 - 4 = 0
=>1/4m -1 +2m +9 - 4 =0
=>9/4m +4 =0
=>9/4m = -4
=>m =-16/9
Vậy ...
TT
0
Tìm được m = 1 hoặc m = -5.