Cho hình bình hành ABCD, A ^ > 90 0 . Kẻ A H ⊥ C D tại H, A K ⊥ B C tại K. Chứng minh
a) A H A K = D A D C ;
b) A K H ^ = A C H ^ .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
30 tháng 10 2018
Đúng(0)
Những câu hỏi liên quan
7 tháng 10 2021
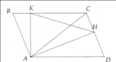
a: Xét ΔADH vuông tại H và ΔCBK vuông tại K có
AD=BC
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔADH=ΔCBK
Suy ra:AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
27 tháng 10 2021
b: Xét ΔADK vuông tại K và ΔCBH vuông tại H có
AD=CB
\(\widehat{ADK}=\widehat{CBH}\)
Do đó: ΔADK=ΔCBH
Suy ra: DK=BH
Xét tứ giác BKDH có
DK//BH
DK=BH
Do đó: BKDH là hình bình hành
CM
30 tháng 3 2018
a) Ta chứng minh
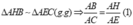
b) Tương tự câu a ta chứng minh được
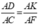
Þ AD.AF =AK.AC (2)
b) Từ (1) ta có AB.AE = AC.AH (3)
Lấy (3) + (2) ta được AD.AF + AB.AE = AC2 (ĐPCM)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
9 tháng 3 2021
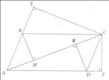
a/ Xét tg vuông AHD và tg vuông AKB có
\(\widehat{BAK}+\widehat{ABC}=90^o\)
\(\widehat{DAH}+\widehat{ADC}=90^o\)
Mà \(\widehat{ABC}=\widehat{ADC}\) (Hai góc đối của hbh)
\(\Rightarrow\widehat{DAH}=\widehat{BAK}\)
=> tg AHD đồng dạng với tg AKB \(\Rightarrow\frac{AH}{AK}=\frac{DA}{AB}\) mà AB = DC (hai cạnh đối của hbh) \(\Rightarrow\frac{AH}{AK}=\frac{DA}{DC}\left(dpcm\right)\)
b/ Ta có K và H đều nhìn AC dưới 1 góc 90 độ
=> Tứ giác AKCH là tứ giác nội tiếp đường tròn đường kính AC
=> sđ \(\widehat{AKH}\) = sđ \(\widehat{ACH}\) = 1/2 sđ cung AH (Góc nội tiếp đường tròn) \(\Rightarrow\widehat{AKH}=\widehat{ACH}\left(dpcm\right)\)
27 tháng 9 2018
Xem ở đây nha:
Cho hình bình hành ABCD, Gọi H và K lần lượt là hình chiếu của A và C lên đường chéo BD. a) Chứng minh AHCK là hình bình hành. b) Gọi O là trung điểm của HK. Chứng minh ba điểm A, O, C thẳng hàng - Toán học Lớp 8 - Bài tập Toán học Lớp 8 - Giải bài tập Toán học Lớp 8 | Lazi.vn - Cộng đồng Tri thức & Giáo dục
27 tháng 9 2018
Xét tam giác vuông ADH & tam giác vuông CKB:
AD = BC ( ABCD là hbh)
góc D1= góc B1 ( so le trong)
=> tam giác vuông = tam giác vuông CKB ( cạnh hyền - góc nhọn)
=> AH = CK ( 2 cạnh t/ứng)
Xét tứ giác AHCK :
AH = CK (cmt)
AH // CK ( cùng vuông góc vs BD)
=> AHCK là hình bình hành ( đn)
13 tháng 6 2023
a: Xét ΔBMC vuông tại M và ΔDNC vuông tại N có
góc B=góc D
=>ΔBMC đồng dạng vớiΔDNC
b: Bạn ghi lại đề đi bạn
16 tháng 12 2021
a: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó: ABCD là hình bình hành
