
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




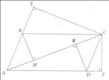
a: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó: ABCD là hình bình hành

a: Xét ΔADH vuông tại H và ΔCBK vuông tại K có
AD=BC
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔADH=ΔCBK
Suy ra:AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành

a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
góc BAC=90 độ
=>ABDC là hình chữ nhật
b: Gọi giao của AH và BC là N
=>N là trung điểm của AH
=>BN là phân giác của góc ABH
=>góc ABN=góc HBN
=>góc HBC=góc ABN=góc DCB
c: Xet ΔAHD có
N,M lần lượt là trung điểm của AH,AD
nên NM là đường trung bình
=>NM//DH và NM=DH/2
=>DH//BC
mà góc DCB=góc HBC
nên DHBC là hình thang cân

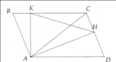
a) Ta chứng minh
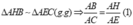
b) Tương tự câu a ta chứng minh được
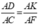
Þ AD.AF =AK.AC (2)
b) Từ (1) ta có AB.AE = AC.AH (3)
Lấy (3) + (2) ta được AD.AF + AB.AE = AC2 (ĐPCM)