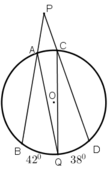
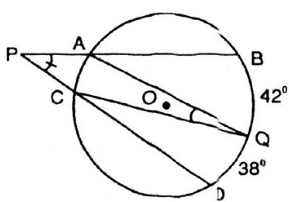
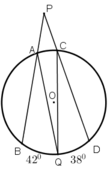
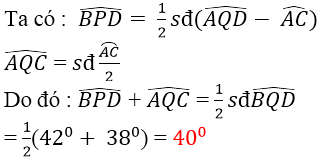Từ một điểm P ở ngoài đường tròn (O), kẻ cát tuyến PAB và PCD tới đường tròn. Gọi Q là một điểm nằm trên cung nhỏ BD (không chứa A và C) sao cho sd BQ ^ = 42 ° ; sd QD ^ = 38 ° . Tính tổng BPD ^ + AQC ^
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
10 tháng 7 2018
Đúng(0)
Những câu hỏi liên quan
25 tháng 4 2017
Hướng dẫn làm bài:
Ta có ˆBPDBPD^ là góc ở ngoài đường tròn (O) nên:
ˆBPD=sđcungBQD−sđcungAC2BPD^=sđcungBQD−sđcungAC2
Ta có ˆAQCAQC^ là góc nội tiếp trong đường tròn (O) nên:
ˆAQC=12sđcungACAQC^=12sđcungAC
Do đó:
ˆBPD+ˆAQC=sđcungBQF−sđcungAC2+sđcungAC2=sđcungBQD2=420+3802=400BPD^+AQC^=sđcungBQF−sđcungAC2+sđcungAC2=sđcungBQD2=420+3802=400
Vậy ˆBPD+ˆAQC=400
AH
Akai Haruma
Giáo viên
15 tháng 3 2021
Bài này bạn đã đăng rồi mà? Bạn vui lòng không đăng 1 bài nhiều lần gây loãng box toán!!!
15 tháng 3 2021
a) Xét (O) có
\(\widehat{ADC}\) là góc nội tiếp chắn \(\stackrel\frown{AC}\)
\(\widehat{PAC}\) là góc tạo bởi tiếp tuyến PA và dây cung AC
Do đó: \(\widehat{ADC}=\widehat{PAC}\)(Hệ quả)
hay \(\widehat{ADP}=\widehat{CAP}\)
Xét ΔADP và ΔCAP có
\(\widehat{ADP}=\widehat{CAP}\)(cmt)
\(\widehat{APD}\) chung
Do đó: ΔADP∼ΔCAP(g-g)
Suy ra: \(\dfrac{PD}{PA}=\dfrac{PA}{PC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(PA^2=PC\cdot PD\)(đpcm)
14 tháng 3 2021
b, Dễ CM được \(\widehat{PAB}=\widehat{PQB}\) (Cm được 5 điểm P, A, O, Q, B thuộc đường tròn theo tứ giác nt)
Mà \(\widehat{PAB}=\widehat{AFB}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nt cùng chắn cung \(\stackrel\frown{AB}\))
\(\Rightarrow\) \(\widehat{PQB}=\widehat{AFB}\)
Mà 2 góc ở vị trí đồng vị \(\Rightarrow\) AF // CD (đpcm)
Chúc bn học tốt!
AH
Akai Haruma
Giáo viên
31 tháng 3 2021
Lời giải:
a) Xét tam giác $PAC$ và $PDA$ có:
$\widehat{P}$ chung
$\widehat{PAC}=\widehat{PDA}$ (góc tạo bởi tiếp tuyến và dây cung thì bằng góc nội tiếp chắn cung đó)
$\Rightarrow \triangle PAC\sim \triangle PDA$ (g.g)
$\Rightarrow \frac{PA}{PC}=\frac{PD}{PA}\Rightarrow PA^2=PC.PD$ (đpcm)
b) Vì $Q$ là trung điểm $CD$ nên $OQ\perp CD$
$\Rightarrow \widehat{PQO}+\widehat{PBO}=90^0+90^0=180^0$
$\Rightarrow PQOB$ là tứ giác nội tiếp
$\Rightarrow \widehat{PQB}=\widehat{POB}=\frac{1}{2}\widehat{AOB}=\widehat{AFB}$ (tính chất góc ở tâm và góc nội tiếp cùng chắn 1 cung)
Mà 2 góc này ở vị trí đồng vị nên $AF\parallel CD$ (đpcm)
12 tháng 3 2023
a: góc SAM=góc SAB+góc BAM
góc SMA=góc SCA+góc MAC
mà góc SAB=góc SCA và góc BAM=góc CAM
nên góc SAM=góc SMA
=>SM=SA
b: góc SGO=90 độ
Vì góc SAO=góc SGO
=>SAGO nọpi tiếp
=>góc SGA=góc SOA=1/2*góc DOA=1/2*sđ cung AD
=>góc SAD=góc SGA
=>ΔSAF đồng djng với ΔSGA
=>SA/SG=SF/SA
=>SA^2=SG*SF
