Trong các khẳng định dưới đây, khẳng định nào sai?
A. l o g a ⇔ 0 < a < 1
B. l n a > 0 ⇔ a > 1
C. log 1 2 a > log 1 2 b ⇔ a > b > 0
D. log 1 5 a = log 1 5 b ⇔ a = b > 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có:
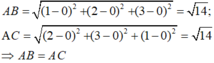
Ta thấy tam giác ABC cân tại đỉnh A. Do đó, AD đồng thời là đường cao của tam giác ABC nên các khẳng định A, B và C đều đúng.
Vậy khẳng định D sai.

Đáp án D
Ta có thể thấy ngay rằng các khẳng định A và C đều đúng.
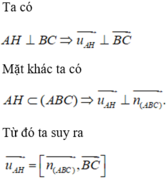
là một vectơ chỉ phương của đường thẳng AH.
Vậy D là khẳng định sai.

Câu D sai, vì khẳng định đó chỉ đúng khi a > 1
Và khi 0 < a < 1 ⇒ logab > logac ⇔ b < c
Chọn D.

Câu D sai, vì khẳng định đó chỉ đúng khi a > 1, còn khi 0 < a < 1 ⇒ logab > logac ⇔ b < c
Chọn D.
Đáp án C
log 1 2 a > log 1 2 b ⇔ a > b > 0.