Tìm x và y biết x2 - 4x + 5 + y2 + 2y = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 10 2021
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{-5}=\dfrac{-3x+2y}{-12-10}=\dfrac{55}{-22}=\dfrac{-5}{2}\)
Do đó: \(\left\{{}\begin{matrix}x=\dfrac{-20}{2}=-10\\y=\dfrac{25}{2}\end{matrix}\right.\)
b: Ta có: \(\dfrac{x}{y}=\dfrac{-7}{4}\)
nên \(\dfrac{x}{-7}=\dfrac{y}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{-7}=\dfrac{y}{4}=\dfrac{4x-5y}{-28-20}=\dfrac{72}{-48}=\dfrac{-3}{2}\)
Do đó: \(\left\{{}\begin{matrix}x=\dfrac{21}{2}\\y=\dfrac{-12}{2}=-6\end{matrix}\right.\)
CM
4 tháng 6 2019
Cách 1 : Xác định các hệ số a, b, c.
a) x2 + y2 – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2
⇒ tâm I (1; 1) và bán kính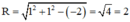 
b) 16x2 + 16y2 + 16x – 8y –11 = 0
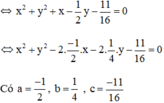
⇒ Đường tròn có tâm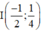 
, bán kính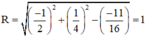 
c) x2 + y2 - 4x + 6y - 3 = 0
⇔ x2 + y2 - 2.2x - 2.(-3).y - 3 = 0
có hệ số a = 2, b = -3,c = -3
⇒ Đường tròn có tâm I(2 ; –3), bán kính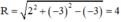 
Cách 2 : Đưa về phương trình chính tắc :
a) x2 + y2 - 2x - 2y - 2 = 0
⇔ (x2 - 2x + 1) + (y2 - 2y +1) = 4
⇔(x-1)2 + (y-1)2 = 4
Vậy đường tròn có tâm I(1 ; 1) và bán kính R = 2.
b) 16x2 + 16y2 + 16x - 8y - 11 = 0
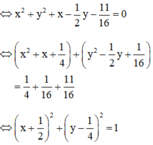
Vậy đường tròn có tâm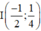 
và bán kính R = 1.
c) x2 + y2 - 4x + 6y -3 = 0
⇔ (x2 - 4x + 4) + (y2 + 6y + 9) = 4 + 9 + 3
⇔ (x - 2)2 + (y + 3)2 = 16
Vậy đường tròn có tâm I( 2 ; –3) và bán kính R = 4.
CM
6 tháng 3 2017
(S) có tâm I(2;1;-1) và bán kính R = m 2 + 2 m + 1 = m + 1
Giao tuyến của (a) và (S) là đường tròn
⇔ d I a < R ⇔ m + 1 > 3 ⇔ m < - 4 m > 2
Đáp án D
10 tháng 3 2022
a: \(=3x^4+3x^2y^2+2x^2y^2+2y^4+y^2\)
\(=\left(x^2+y^2\right)\left(3x^2+2y^2\right)+y^2\)
\(=3x^2+3y^2=3\)
b: \(=7\left(x-y\right)+4a\left(x-y\right)-5=-5\)
c: \(=\left(x-y\right)\left(x^2+xy+y^2\right)+xy\left(y-x\right)+3=3\)
d: \(=\left(x+y\right)^2-4\left(x+y\right)+1\)
=9-12+1
=-2
CM
2 tháng 9 2019
Đáp án A
Ta có, giả thiết log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ x 2 + y 2 + 3 ≤ 2 x + 2 y + 5 ⇔ x - 1 2 + y - 1 2 ≤ 4 là miền trong đường tròn tâm I(1;1) bán kính R 1 = 2
Và x 2 + y 2 + 4 x + 6 y + 13 - m = 0 ⇔ x + 2 2 + y + 3 2 = m là đường tròn tâm I(-2;-3); R 2 = m
Khi đó, yêu cầu bài toán ⇔ R 1 + R 2 = I 1 I 2 ⇔ m + 2 = 5 ⇔ m = 9
CM
21 tháng 2 2019
Đáp án A
Ta có, giả thiết
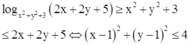
là miền trong đường tròn tâm I(1;1) bán kính R1 = 2
Và
X = 2
Y= -1