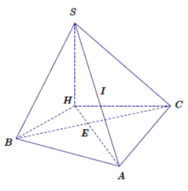
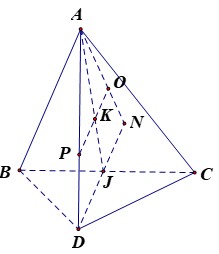
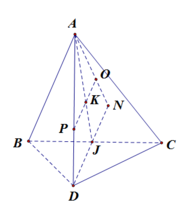
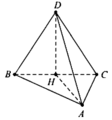
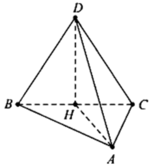
Cho tứ diện ABCD có ABC là tam giác cân tại A, người ta để một quả cầu có bán kính r = 1 vào bên trong tứ diện từ đáy ABC sao cho các cạnh AB, BC, CA lần lượt tiếp xúc với quả cầu và phần quả cầu bên trong tứ diện có thể tích bằng phần quả cầu bên ngoài tứ diện. Biết khoảng cách từ D đến (ABC) bằng 2. Tính thể tích nhỏ nhất của tứ diện ABCD?
![]()
![]()
![]()
![]()






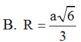
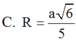
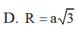

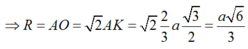

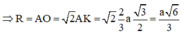
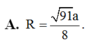
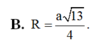
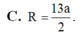


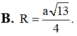
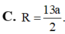
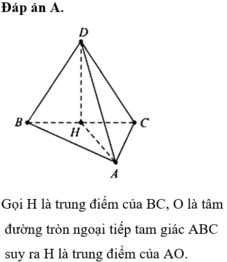

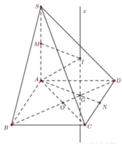

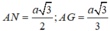


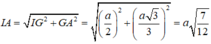
Đáp án C
Tứ diện ABCD có chiểu cao không đổi do đó thể tích nhỏ nhất khi diện tích tam giác ABC nhỏ nhất. Vì AB, BC, CA lần lượt tiếp xúc với quả cầu và phần quả cầu bên trong tứ diện có thể tích bằng phần quả cầu bên ngoài tứ diện nên tâm I của mặt cầu nằm trong tam giác ABC