Cho tứ giác ABCD nội tiếp đường tròn (O) (hình 1) . Chọn khẳng định sai?
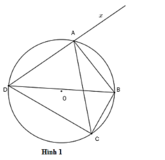
A. B D C ^ = B A C ^
B. A B C ^ + A D C ^ = 180 0
C. D C B ^ = B A x ^
D. B A C ^ = B A x ^
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D

(góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó )
Phương án A, B, C đúng

1. AB // CD (ABCD là hình thang) => ^B + ^D = 180o (Trong cùng phía)
Mà ^B = ^A (ABCD là hình thang) => ^A + ^D = 180o
Xét hình thang ABCD có: ^A đối diện với ^D
^A + ^D = 180o (cmt)
=> hình thang ABCD nội tiếp đường tròn
2. Xét hình chữ nhật LMNO có:
^L + ^N = 180o (^L = 90o; ^N = 90o)
=> hình chữ nhật LMNO nội tiếp đường tròn
3. Xét hình vuông PQRS có:
^P + ^R = 180o (^P = 90o; ^R = 90o)
=> hình vuông PQRS nội tiếp đường tròn

Chọn đáp án D
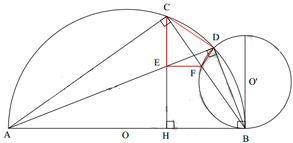

* Gọi (O’) là đường tròn đi qua D và tiếp xúc với AB tại B.
Đường tròn (O’) cắt CB tại F khác B. Chứng minh E F / / A B .
Ta có:

Hai góc ở vị trí đồng vị ⇒ E F / / A B

b) Xét ΔFDC có
A\(\in\)FD(gt)
B\(\in\)FC(gt)
AB//CD(gt)
Do đó: \(\dfrac{FA}{AD}=\dfrac{FB}{BC}\)(Định lí Ta lét)
\(\Leftrightarrow\dfrac{FA}{FB}=\dfrac{AD}{BC}=1\)
hay FA=FB
Ta có: FA+AD=FD(A nằm giữa F và D)
FB+BC=FC(B nằm giữa F và C)
mà FA=FB(cmt)
và AD=BC(ABCD là hình thang cân)
nên FD=FC
Ta có: FA=FB(cmt)
FD=FC(cmt)
Do đó: \(FA\cdot FD=FB\cdot FC\)(đpcm)
a) Ta có: ABCD là tứ giác nội tiếp(gt)
nên \(\widehat{A}+\widehat{C}=180^0\)(hai góc đối)(1)
Ta có: ABCD là hình thang(AB//CD)
nên \(\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)(2)
Từ (1) và (2) suy ra \(\widehat{C}=\widehat{D}\)
Hình thang ABCD(AB//CD) có \(\widehat{C}=\widehat{D}\)(cmt)
nên ABCD là hình thang cân(Dấu hiệu nhận biết hình thang cân)
Chọn đáp án D
(góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó )
Phương án A, B, C đúng