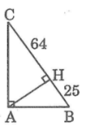
Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 25cm, HC = 64cm. Tính góc B , C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Q
1
24 tháng 8 2021
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=40cm\\AC=8\sqrt{89}cm\end{matrix}\right.\)
Xét ΔACH vuông tại H có
\(\sin\widehat{C}=\dfrac{AH}{AC}=\dfrac{5}{\sqrt{89}}\)
\(\Leftrightarrow\widehat{C}\simeq32^0\)
hay \(\widehat{B}=58^0\)
O
6
15 tháng 6 2019
Tam giác ABC vuông ở A, ta có:
AH2 = 25.64 = 1600, suy ra AH = 40 (cm).
\(tgB=\frac{AH}{BH}=\frac{40}{25}=1,6\)
=> \(\widehat{B}\approx58^0\); \(\widehat{C}=32^0\).
15 tháng 6 2019
hình đây nha
Ta có : AH^2 = CH . HB
=>AH=40
Ta lại có:tan B = AH / HB=40/25=1.6
=>B = 580
=>C = 320
27 tháng 5 2023
a: BC=25+64=89cm
AH=căn 25*64=40cm
S ABC=1/2*40*89=1780cm2
AB=căn 25*89=5căn 89cm
AC=căn 64*89=8 căn 89
=>C=13căn 89+89(cm)
b: tan B=AC/AB=8/5
=>góc B=58 độ
=>góc C=32 độ
c:
góc AMH=góc ANH=góc MAN=90 độ nên AMHN là hcn
=>MN=AH=40cm
CM
12 tháng 10 2017
Đáp án C
Ta có: BC = HB + HC = 25 + 64 = 89 cm
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
TP
1
2 tháng 10 2021
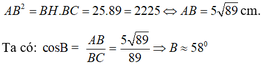
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=HB\cdot HC\)
hay AH=40(cm)
Xét ΔABH vuông tại H có
\(\tan\widehat{B}=\dfrac{AH}{HB}=\dfrac{40}{25}=\dfrac{8}{5}\)
\(\Leftrightarrow\widehat{B}\simeq58^0\)
hay \(\widehat{C}=32^0\)
3 tháng 4 2023
a: Xét ΔABC vuông tại A có AH là đường cao
nên AC^2=CH*CB
b: \(BC=25+36=61\left(cm\right)\)
\(AB=\sqrt{25\cdot61}=5\sqrt{61}\left(cm\right)\)
=>A\(C=6\sqrt{61}\left(cm\right)\)
21 tháng 9 2019
Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
A H 2 = H B . H C
Suy ra: