Có 7 nhà toán học nam, 4 nhà toán học nữ và 5 nhà vật lý nam.Có bao nhiêu cách lập đoàn công tác gồm 3 người có cả nam và nữ đồng thời có cả toán học và vật lý.
A.210
B.314
C. 420
D. 213
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 5 2019
Ta có các khả năng sau
- Đoàn công tác gồm: 1 nhà toán học nữ, 1 nhà vật lý và 1 nhà toán học nam
Số cách chọn: C 7 1 . C 4 1 . C 5 1 = 140 cách
- Đoàn công tác gồm: 1 nhà toán học nữ, 2 nhà vật lý
Số cách chọn: C 4 1 . C 5 2 = 40 cách
- Đoàn công tác gồm: 2 nhà toán học nữ, 1 nhà vật lý
Số cách chọn: C 4 2 . C 5 1 = 30 cách
Vậy số cách lập là: 140 + 40 + 30 = 210 cách.
Chọn đáp án A.
CM
11 tháng 5 2017
Đáp án A.
* Hướng dẫn giải:
+ Đoàn công tác gồm: 1 nhà toán học nữ, 1 nhà vật lý và 1 nhà toán học nam
Số các để chọn: 
cách
+ Đoàn công tác gồm: 1 nhà toán học nữ, 2 nhà vật lý
Số cách chọn: 
cách
+ Đoàn công tác gồm: 2 nhà toán học nữ, 1 nhà vật lý
Số cách chọn: 
cách
Vậy số cách lập là: 210 cách
CM
20 tháng 7 2017
Đáp án B
Th1 : Số cách chọn ra 1 nhà toán học nam, 1 nhà toán học nữ, 1 nhà vật lý nam : 5.3.4 = 60
Th2 : Số cách chọn ra 2 nhà toán học nữ, 1 nhà vật lý nam : C 3 2 . C 4 1 = 12
Th3 : Số cách chọn ra 1 nhà toán học nữ, 2 nhà vật lý nam : C 3 1 C 4 2 = 18
Vậy có số cách chọn là : 90.
CM
12 tháng 12 2018
Đáp án B
Th1 : Số cách chọn ra 1 nhà toán học nam, 1 nhà toán học nữ, 1 nhà vật lý nam : 5.3.4 = 60
Th2 : Số cách chọn ra 2 nhà toán học nữ, 1 nhà vật lý nam : C 3 2 C 4 1 = 12
Th3 : Số cách chọn ra 1 nhà toán học nữ, 2 nhà vật lý nam : C 3 1 C 4 2 = 18
Vậy có số cách chọn là : 90
PL
2 tháng 8 2021
th1: chọn 1 nhà toán học nam, 1 nhà toán học nữ, 1 nhà vật lý nam
có: 5.3.4 = 60 (cách chọn)
th2: chọn 2 nhà toán học nữ, 1 nhà vật lý nam
có: 3C2.4C1 = 12 (cách chọn)
th3: chọn 1 nhà toán học nữ, 2 nhà vật lý nam
có: 3C1.4C2 = 18 (cách chọn)
vậy có tổng cộng 60 + 12 + 18 = 90 cách chọn
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2022
a.
Chọn 1 nam từ 9 nam có 9 cách
Chọn 1 nữ từ 3 nữ có 3 cách
\(\Rightarrow\) Có \(9.3=27\) cách chọn nhóm 1 nam 1 nữ
b.
Chọn 2 nhà toán học từ 8 nahf toán học: \(C_8^2\) cách
Chọn 2 nhà vật lý từ 4 nhà vật lý: \(C_4^2\) cách
\(\Rightarrow C_8^2.C_4^2\) cách lập
c.
Các trường hợp thỏa mãn: (1 nhà toán học nữ, 2 nhà vật lý nam), (1 nhà toán học nữ, 1 nhà toán học nam, 1 nhà vật lý nam), (2 nhà toán học nữ, 1 nhà vật lý nam)
\(\Rightarrow C_3^1.C_4^2+C_3^1.C_5^1.C_4^1+C_3^2.C_4^1\) cách
CM
20 tháng 10 2018
Chọn C.
Số cách chọn 4 nhà khoa học mà có đủ cả ba lĩnh vực là
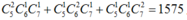
Số cách chọn 4 nhà khoa học nam mà có đủ cả ba lĩnh vực là
Số cách chọn 4 nhà khoa học nữ mà có đủ cả ba lĩnh vực là
Vậy số cách lập một ban thư kĩ thỏa mãn yêu cầu là:
Ta có các khả năng sau
Đoàn công tác gồm: 1 nhà toán học nữ, 1 nhà vật lý và 1 nhà toán học nam
Số cách chọn: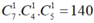
cách
Đoàn công tác gồm: 1 nhà toán học nữ, 2 nhà vật lý
Số cách chọn: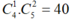
cách
Đoàn công tác gồm: 2 nhà toán học nữ, 1 nhà vật lý
Số cách chọn: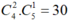
cách
Vậy số cách lập là: 210 cách.
Chọn A.