Các hình tứ giác có trong hình trên là:
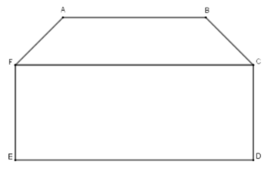
A. Hình tứ giác ABCF và hình tứ giác CDEF
B. Hình tứ giác ABCF; CDEF và ABCDEF
C. Hình tứ giác ABCF
D. Hình tứ giác ABCD và hình tứ giác CDEF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,Xét tứ giác ABDC có:
D đối xứng với A qua M nên :
DA=DC(1)
M là trung điểm BC nên:
BM=MC(2)
Từ (1)và (2) suy ra:
tứ giác ABDC là hình chữ nhật(đpcm)
b, vì ABDC là hình chữ nhật nên:
AB=DC và AB//DC
mà DC=FC và F trên tia DC
=>AB=FC và AB//FC
vậy tứ giác ABCF là hình bình hành(đpcm)

a)
Ta có: MB=MF(gt)
mà F,B,M thẳng hàng
nên M là trung điểm của BF
Xét tứ giác ABCF có
M là trung điểm của đường chéo AC(gt)
M là trung điểm của đường chéo BF(cmt)
Do đó: ABCF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Ta có: ABCF là hình bình hành(cmt)
nên AF//BC(Hai cạnh đối trong hình bình hành ABCF)
hay AD//CE
Ta có: ΔABC vuông tại A(gt)
mà AE là đường trung tuyến ứng với cạnh BC(E là trung điểm của BC)
nên \(AE=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(CE=\dfrac{BC}{2}\)(E là trung điểm của BC)
nên AE=CE
Xét tứ giác AECD có
AD//CE(cmt)
AD=CE(cmt)
Do đó: AECD là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành AECD có AE=CE(cmt)
nên AECD là hình thoi(Dấu hiệu nhận biết hình thoi)
C,
kẻ MN
Xét tam giác ABC có
N là trung điểm AB ( Gt)
M là trung điểm AC( gt)
-> MN là đg trung bình tam giác ABC
-> MN song song BC
Ta có MN song song BC
mà BC ⊥ BI ( gt)
-> Mn ⊥BI hay Mn là đg cao
Xét tam giác BIM có
BA là đg cao do( tam giác ABC vuông tại A- gt)
MN là đg cao ( cmt)
-> N là trực tâm tam giác BIA
-> IN là đg cao thứ 3 trong tam giác BIM hay IN ⊥ BM( đpcm)
LIke nha bn![]()
cho hình bình hành ABCD.lấy điểm e thuộc BD sao cho BE=DF. chứng minh tứ giác ABCF là hình bình hành


a: Xét tứ giác ABEC có
M là trung điểm của đường chéo BC
M là trung điểm của đường chéo AE
Do đó: ABEC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABEC là hình chữ nhật

Đặt ê ke như hình vẽ để kiểm tra xem mỗi tứ giác có hay không hai cạnh song song.
+ Tứ giác ABCD có AB // CD nên là hình thang.
+ Tứ giác EFGH không có hai cạnh nào song song nên không phải hình thang.
+ Tứ giác KMNI có KM // IN nên là hình thang.
Hình đã cho có các hình tứ giác là: ABCF và CDEF.
Đáp án cần chọn là A