Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Phương trình hoành độ giao điểm của đồ thị (C) và trục hoành : x 4 + 4 x 2 = 0 ⇔ x = 0 . Vậy đồ thị (C) và trục hoành có 1 giao điểm
Đáp án C.
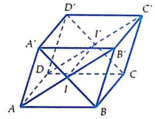
+ A D C ' B ' là hình bình hành.
+ I I ' / / A D ⇒ I I ' / / A D D ' A ' và I I ' → = A D → nên đáp án A, B là đúng.
+ I I ' / / A B C D nên I I ' và DC không có điểm chung nên đáp án D đúng.
+ A B B ' A ' / / B C C ' B ' = B B ' và A D C ' B ' ∩ B C D ' A ' = I I ' tức là I I ' và B B ' không cùng thuộc một mặt phẳng nên đáp án C sai.
Đáp án là B.
Phương trình hoành độ giao điểm của P và (C):
x 4 − 6 x 2 + 3 = − x 2 − 1 ⇔ x 4 − 5 x 2 + 4 = 0 ⇔ x 2 = 1 x 2 = 4 ⇔ x = ± 1 x = ± 2
Vậy ta có tổng bình phương các hoành độ giao điểm của P và (C): − 1 2 + 1 2 + − 2 2 + 2 2 = 10
Đáp án A.
Số giao điểm của 2 đồ thị là số nghiệm của phương trình hoành độ giao điểm
x4 – 2x2 = x2 – 2 <=> x4 – 3x2 + 2 = 0
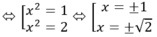
Vậy có 4 giao điểm của 2 đồ thị đã cho.
Đáp án A.
Phương trình hoành độ giao điểm là
x4 – 2x2 = x2 – 2 <=> x4 – 3x2 + 2 = 0
Vậy có 4 giao điểm của hai đồ thị.
Đáp án A.
Phương trình hoành độ giao điểm:
x4 – 4x2 – 2 = 1 – x2 ⇔ x4 – 3x2 – 3 = 0